Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 56

Uma criança tem um montante fixo para comprar latinhas de refrigerantes e cachorros quentes para sua festa de aniversário. Suponha que cada latinha de refrigerante custe e cada cachorro quente .

a) Obtenha a equação de restrição orçamentária.

b) Esboce o gráfico, supondo as variáveis contínuas.

c) Se a criança optar em usar todo seu orçamento comprando somente cachorros quentes, estime o número de cachorros quentes que podem ser comprados.

Passo 1

a) Então pessoal, para escrevermos uma equação de restrição orçamentária é bem tranquilo, tá? O modelo para uma equação desse tipo é a seguinte:

No nosso caso, temos que é o custo dos refrigerantes e é o custo dos cachorros-quentes. Como vão ser comprados vários refrigerantes e cachorros-quentes e sabemos quanto custa cada um, teremos que:

No qual:

preço do refrigerante;

quantidade de refrigerantes;

preço do cachorro-quente;

quantidade de cachorros-quentes.

Sendo assim, nossa equação será:

Aqui vale ressaltar que o montante é , assim como dito pelo enunciado! 😉

Passo 2

b) Então galera, para esboçar o gráfico temos que assumir uma variável de quantidade em função da outra, certo? Vamos fazer , ok? Se isolarmos na equação, teremos:

Sendo assim, se plotarmos o gráfico dessa função, teremos:

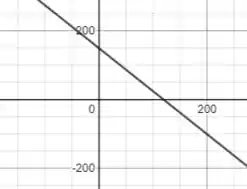
No qual o eixo vertical é e o eixo horizontal é .

Passo 3

c) Se a criança utilizar todo o dinheiro para comprar cachorros quentes, então temos que , correto? Utilizando a expressão do passo anterior, teremos:

Então ela poderá comprar cachorros-quentes com o dinheiro! 😊

Resposta

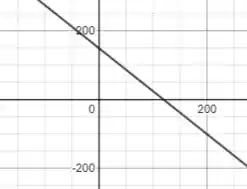
c) cachorros-quentes

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tabela mostra a média mundial de consumo de petróleo desde 1985 até 2010, medida em milhares de barris por dia.a) Faça um gráfico com os pontos da tabela e diga se um modelo linear é apropriado.b) F

Antropologistas usam um modelo linear que relaciona altura do fêmur humano com sua altura. O modelo permite a um antropologista determinar a altura de um individuo quando apenas parte do esqueleto (in

Faça o gráfico da função a mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = 1 - 1 x

Faça o gráfico da função a mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = - x 2

Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.y = 3 - 2 c o s x