O custo total de uma plantação de sejoga é uma função em geral, da área cultivada. Uma parcela do custo é aproximadamente constante (custos fixos) e diz respeito às benfeitorias e equipamentos necessários. A outra parcela diz respeito aos custos dos insumos e mão-de-obra e depende da área plantada (custos variáveis). Supor que os custos fixos sejam de e os custos variáveis sejam de por hectare.
a) Determinar o custo total da plantação em função do número de hectares plantados.
b) Fazer um esboço do gráfico da função custo total.
c) Como podemos visualizar os custos fixos e variáveis no gráfico?
Passo 1
a) Então galera, a questão já nos dá um bom indicativo de como será a função do custo total em função do número de hectares plantados. Os custos fixos são de e os variáveis são por hectare, sendo assim já sabemos que a função será linear, do tipo:
No nosso caso , então:
No qual número de hectares plantados.
Passo 2
b) Aqui nessa questão não tem nenhum segredo, não é mesmo? Basta plotarmos o gráfico da expressão que escrevemos no passo anterior, se liga:
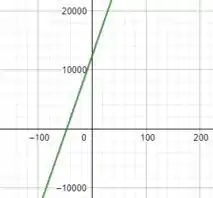
Que se trata de um gráfico do custo total em função dos hectares plantados .
Passo 3
c) Então pessoal, observando o gráfico que plotamos no passo anterior com bastante cuidado, podemos concluir que:
O custo fixo é dado pelo ponto aonde a reta corta o eixo vertical , que é exatamente em .
O custo variável pode também ser chamado de coeficiente angular da função , e o coeficiente angular é dado pela razão entre o comprimento do segmento vertical (em roxo) e o comprimento do seguimento horizontal (em azul), que estão representados na figura abaixo:
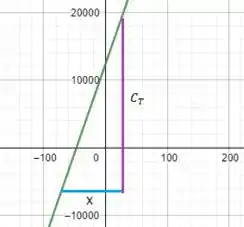
Em outras palavras, o custo fixo é o segmento em azul e o custo variável é o segmento em roxo.
Resposta
a)
b) 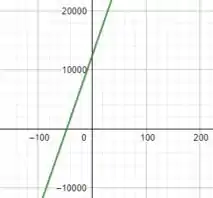
c) 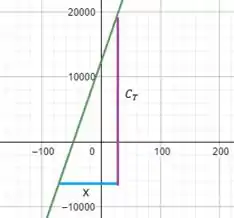
O custo fixo é o segmento em azul e o custo variável é o segmento em roxo.