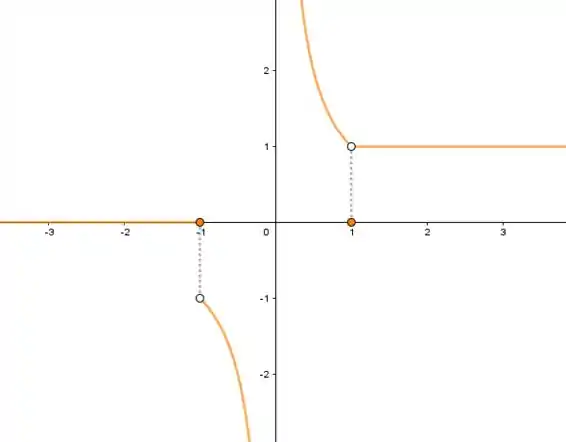
Faça o gráfico da função
Em seguida discuta em detalhes, os limites, limites lateria s continuidade e continuidade lateral de em e . Algumas dessas continuidades é removível? Explique
Passo 1
O primeiro passo é lembrar as definições de continuidade e continuidade lateral. Sendo assim,
Pelo teste de continuidade temos que uma é continua em (ponto qualquer) se e somente se,
- existir (pertencer ao domínio de
- existir ( possui um limite quando )
- (o limite é igual ao valor da função no ponto )
Já para continuidade lateral, temos que é continua no ponto , se
Passo 2
O segundo passo é verificar a continuidade e a continuidade lateral em
Mas para isso temos que analisar com cuidado,
Verificando a continuidade lateral
Quando estamos com valores menores que , então ,
Quando estamos com valores maiores que , então ,pois aplicaremos o módulo ao .
Logo,
Quando isso acontece dizemos que esse limite não existe.
Verificando a continuidade
- Vimos que
Fazendo com que o limite não existisse, sendo assim também não poderá existir.
Portanto, como não existe, então é descontinua em
Passo 3
O terceiro passo é verificar a continuidade e a continuidade lateral em
Para isso temos que avaliar com cuidado,
Verificando a continuidade lateral
Quando estamos com valores menores que zero, então ,pois aplicaremos o módulo ao .
Isso acontece pois estamos com valores negativos.
Quando estamos com valores maiores que zero, então ,pois aplicaremos o módulo ao .
Logo,
Quando isso acontece dizemos que esse limite não existe.
Verificando a continuidade
- não existe, pois não pertence ao domínio da .
Portanto, como não pertence ao domínio da Então é descontinua em
Perceba que zero pertencer ao domínio da , não faz muita diferença pois o papel dele é simplesmente dar um “salto” na função de depois voltar para o caminho que ela estava seguindo, quando isso acontece dizemos que essa descontinuidade é removível
Passo 4
O quarto passo é verificar a continuidade e a continuidade lateral em
Mas para isso temos que analisar com cuidado,
Verificando a continuidade lateral
Quando estamos com valores menores que , então , pois aplicaremos o módulo ao .
Quando estamos com valores maiores que , então ,
Logo,
Portanto, é continua lateralmente em
Verificando a continuidade
- Vimos pela continuidade lateral que
- Porém, quando isso acontece
Se tanto pela esquerda quanto pela direita o limite deram 1 , então
Como então é descontinua em
Perceba que o fato de 1 pertencer ao domínio da , não faz muita diferença pois o papel dele é simplesmente dar um “salto” na função de depois voltar para o caminho que ela estava seguindo, quando isso acontece dizemos que essa descontinuidade é removível
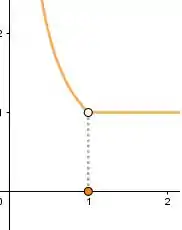
Resposta
é descontinua em e .