Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 60
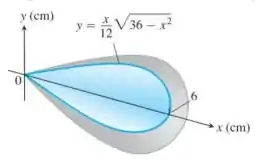
Projeto de um peso para prumo. Você é o encarregado de projetar um peso de latão para prumo que pesará aproximadamente , e decide concebê-lo como o sólido de revolução mostrado aqui. Determine o volume do peso. Se você especificar um latão com densidade , qual será o peso em gramas do prumo (arredonde para o inteiro mais próximo)?
Passo 1
Então galera, para determinarmos o “peso” do prumo (que na verdade seria a massa, mas tudo bem) precisamos utilizar a relação de densidade, uma vez que a questão nos cede a densidade do latão. Sendo assim, teremos a seguinte expressão:
Como a densidade já nos é cedida, então precisamos determinar o volume do sólido, certo? É aí que a resolução entra de fato, mas fiquem tranquilos, não é um bicho de 7 cabeças não, viu?! Bora lá!
Passo 2
Para determinarmos o volume desse sólido, galera, devemos utilizar a equação que o próprio George nos cede na seção 5.4, que é a seguinte:
Para descobrirmos o volume total desse sólido, vamos dividir todo o sólido em discos de larguras infinitesimais para utilizarmos a equação acima, ok? Se fizermos isso, temos que a área de cada disco será:
Sendo assim, nosso volume será:
Mas é aí que está! Quem seria esse ? O próprio desenho do enunciado nos cede esse valor, que é:
Então a integral que teremos que resolver é a seguinte:
Simplificando os expoentes, teremos:
Vale lembrar que o sólido vai de a , assim como podemos notar na figura!
Passo 3
Ufaaa! Agora sim chegamos em uma integral mais bonitinha e mais tranquila de se resolver, não é mesmo? Abrindo essa integral, teremos o seguinte, galera:
Resolvendo a integral, teremos:
Passo 4
Agora que encontramos quanto vale o volume, basta utilizarmos a equação que escrevemos lá no passo 1 para descobrirmos a massa, saca só: