Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 53
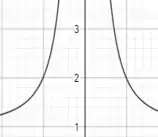
Faça o gráfico da função:
Passo 1
Esse exercício é literalmente a mesma coisa que o exercício anterior, galera! A diferença é que há uma soma ao invés de uma subtração. De início, sabemos que nunca poderá ser 0! Sendo assim, a função vai tender a , mas nunca admitirá esse ponto. Beleza?!
Se pegarmos apenas a função , teremos o seguinte gráfico:
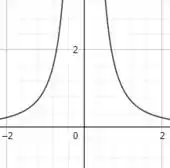
Essa função aparece bastante nos livros de cálculo, pessoal. Então vamos nos atentar bastante a ela, tranquilo?!
Passo 2
Assim como comentado no exercício anterior, se tivermos uma soma ou subtração na função, isso significa que a função vai ser deslocada para cima ou para baixo. Sim, é só isso!
No nosso caso, temos uma soma de uma unidade, então a função vai ser deslocada 1 unidade para cima. Olha só como o gráfico vai ficar:
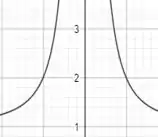
Tranquilão, né?!
Resposta
O gráfico de é:
