Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.2 - Ex. 9
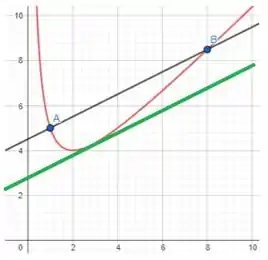
- Faça o gráfico da função na janela retangular por .
- Faça o gráfico da reta secante que passa pelos pontos e na mesma tela que .
- Encontre o número que satisfaça à conclusão do Teorema do Valor Médio para essa função e o intervalo . Então, faça o gráfico da reta no ponto e observe que ela é paralela à reta secante.
Passo 1
Eaee, belezinha??? Bom... a questão é bem direta e pede algumas coisinhas sobre a seguinte função:
Em tão vamos devagarinho aqui em cada passo e analisar o que o enunciado pede, certinho?? 😉
A gente ainda vai precisar do Teorema do Valor Médio, mas lembre-se de já dele:
“O Teorema do Valor Médio afirma que se uma função contínua é diferenciável em um intervalo fechado , então existe pelo menos um ponto em onde a inclinação da reta tangente é igual à inclinação média da função nesse intervalo.”
Passo 2
Letra a).
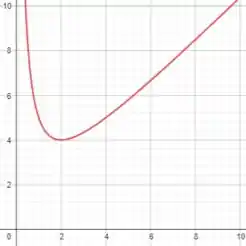
Primeiro vamos plotar a função na janela retangular por :
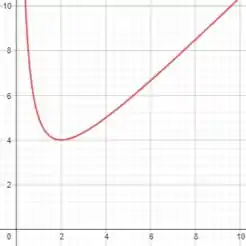
Passo 3
Letra b).
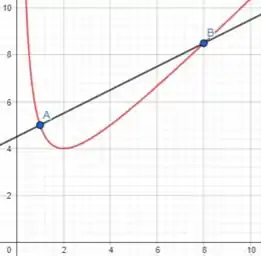
Agora, fazendo o gráfico da reta secante que passa pelos pontos e na mesma tela que , temos:
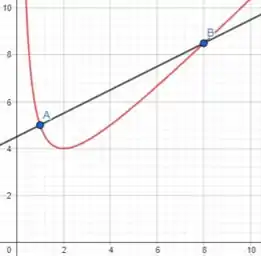
Passo 4
Letra c).
Agora, devemos encontrar o número que satisfaça à conclusão do Teorema do Valor Médio para essa função e o intervalo .
Encontrando o número :
Derivando, temos:
Então, (inclinação da função) e:
Com isso, temos que:
Concluindo, uma equação da linha tangente é
Passo 5
Fazendo o gráfico da reta no ponto
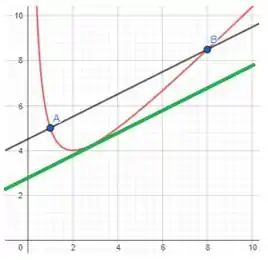
Resposta
a)
b)
c)
