Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.2 - Ex. 3
É mostrado o gráfico da função .
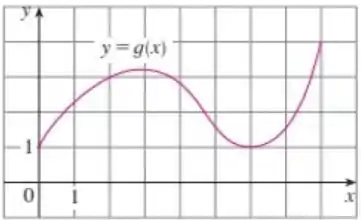
a) Verifique que satisfaz as hipóteses do Teorema do Valor Médio no intervalo .
b) Estime o(s) valor(es) de que satisfazem a conclusão do Teorema do Valor Médio no intervalo .
c) Estime o(s) valor(es) de que satisfazem a conclusão do Teorema de Valor Médio no intervalo .
Passo 1
Opa! Bora pra mais uma questão?! Nessa temos um gráfico dado que é o seguinte:
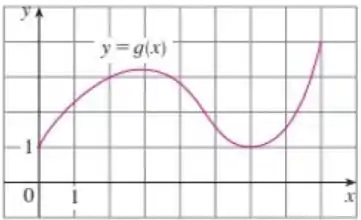
Então temos que investigar se ele satisfaz ao teorema do valor médio e depois vamos estimar o valor de que satisfaça a conclusão desse teorema para o intervalo de e .
O Teorema do Valor Médio diz que:
“Sendo a função que satisfaça às seguintes condições:
- é contínua no intervalo fechado de ;
- é diferenciável no intervalo aberto de ;
Então há um número c no intervalo aberto onde . ”
Em outras palavras, se as condições para no intervalo forem satisfeitas, então existe ao menos um ponto cuja derivada (inclinação da reta tangente) é igual a inclinação da reta secante entre os pontos extremos do intervalo.
Bom, com o teorema fresquinho na nossa cabeça agora, vamos analisar o nosso gráfico.
Passo 2
Observando um gráfico conseguimos perceber que temos uma função polinomial. Isso significa que ela será contínua e diferenciável!
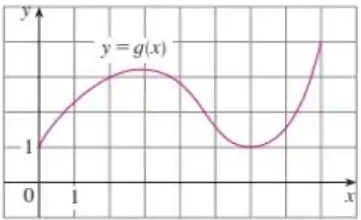
Agora, sabendo que cada quadradinho vale uma unidade, podemos achar os valores de c para os intervalos dados no enunciado.
Se você reparar bem essa é a inclinação da reta secante entre os pontos extremos dos intervalos.
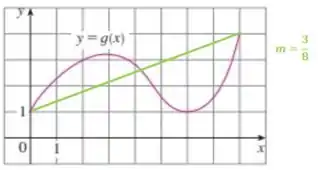
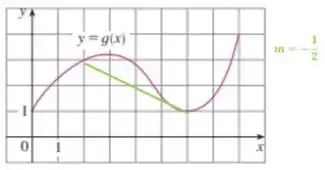
Passo 3
Agora vem a parte mais desafiadora, vamos precisar encontrar os pontos do gráfico onde as derivadas são igual a e .
Para isso, vamos traçar retas tangentes ao gráfico e ver em que pontos essas retas vão ter inclinação igual a da reta secante que traçamos no fim do Passo 2.
Para o primeiro intervalo temos:
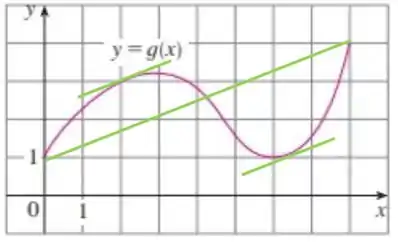
Dessa forma, sendo:
Podemos estimar que:
Agora a mesma coisa pra inclinação .
Eu desenhei uma reta maior, pegando todo o intervalo pra ficar mais visível. Agora procuramos os pontos:
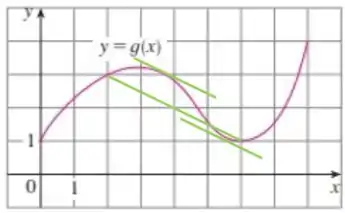
Prontinho!