Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 10
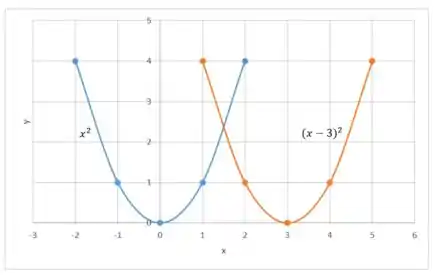
Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.
Passo 1
E aí!? Aqui temos a função:
O problema pede pra a gente consultar a secção 1.2 do livro, achar o gráfico de uma função similar a dada aqui e, a partir dela, usando transformações devemos chegar no gráfico da função acima!
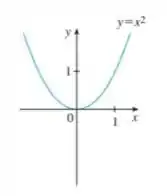
Observando a nossa função vemos que ela se parece com uma função quadrática! Então é nela que a gente vai se basear:
Aqui na secção temos os seguintes tipos de transformações, para :
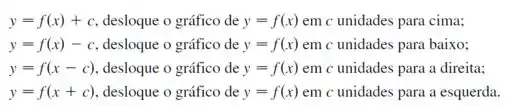
Pra resolver esse tipo de problema vamos investigar que tipo de transformação a gente precisa fazer pra sair de:
E ir para:
Passo 2
Parece que a transformação aqui é do tipo , onde , mas vamos confirmar:
Isso aí! Então tudo que temos que fazer é deslocar o gráfico em 3 unidades pra direita!
Pra ficar mais simples vamos fazer uma tabelinha de podemos com e .
Se o gráfico vai ser deslocado unidades pra direita, então vamos aumentar unidades em cada e como ele não vai se deslocar verticalmente o continua igual. Assim:
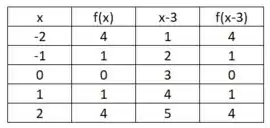
Passo 3
Agora vamos plotar:
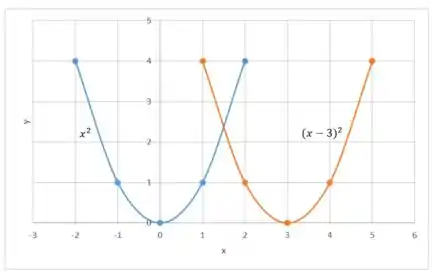
Prontinho!
Resposta
