Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 23
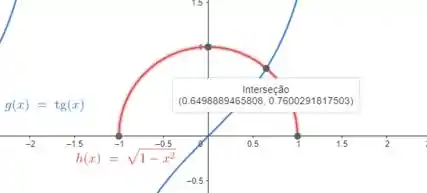
Encontre todas as soluções da equação, com duas casas decimais de precisão
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação:
Com isso, queremos encontrar todas as soluções dessa equação.
Mas olhe bem... resolver isso de forma analítica é complicado né???
Mas calma, não se desespere haha.
Uma ideia é analisar esses dois termos da equação de forma separada e depois juntar eles em uma só função.
Quer saber como?? Bora junto!! 😉
Passo 2
Vamos pensar aqui juntos...
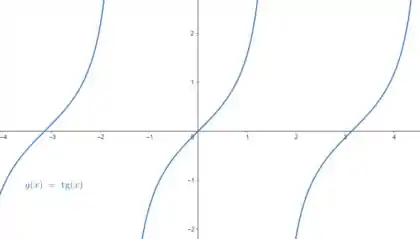
Seja . A gente sabe como se comporta uma tangente no plano cartesiano:
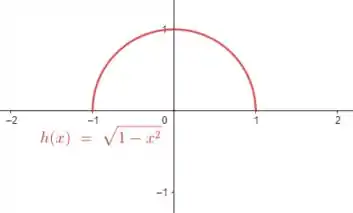
Se fizermos também , percebemos que trata-se de uma função que representa a parte superior de um círculo de raio centrado na origem do plano cartesiano:
Então vamos pensar juntos aqui...
Se igualarmos as duas funções, então quer dizer que os pontos de encontro delas são as raízes!!!
Passo 3
Assim, plotando as duas curvas no mesmo plano cartesiano, obtemos:
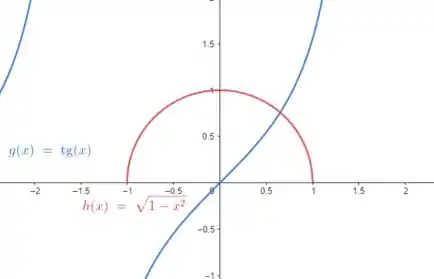
Perceba que só teremos um ponto de encontro!!
Esse ponto ocorre em aproximadamente , veja:
