Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 48a
Usando uma ferramenta gráfica, trace numa mesma janela o gráfico das funções dadas em cada item e, a seguir, responda a questão:
Dado o gráfico de , o que se pode afirmar sobre o gráfico de , quando ? E quando ?
a)
Passo 1
Então pessoal, utilizando uma ferramenta gráfica para plotar os gráficos em uma mesma tela, teremos o seguinte:
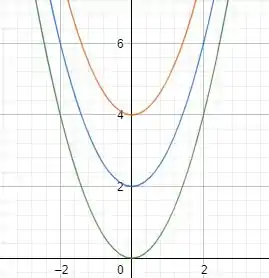
No qual a função em verde é a função ;
A função em azul é a função ;
A função em laranja é a função .
Passo 2
Quando uma função apresenta uma constante, ou seja, um número somando ou subtraindo junto com a variável, o que acontece com o gráfico é que o mesmo vai ser deslocado verticalmente, sendo essa translação para cima ou para baixo! No nosso caso temos que , e como podemos notar o gráfico é deslocado verticalmente para cima!
Quando não podemos analisar nessa questão, uma vez que não temos uma constante negativa!
Resposta
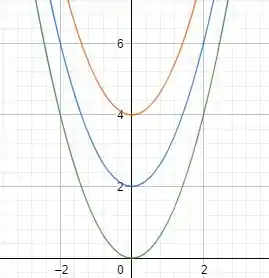
Quando o gráfico é deslocado verticalmente para cima!