Faça o gráfico, inclua as equações das assíntotas e dos termos dominantes
Passo 1
Vamos analisar a função .
Perceba que o ponto não causa um estrago na função, pois ela explode. Então ele é nossa assíntota vertical beleza ?
Precisamos saber como a função se comporta a direita e à esquerda desse ponto, então vamos analisar primeiro à esquerda dele , isto é,
Usando a regra do quociente (o limite do quociente é quociente dos limites),
Usando a regra da subtração (o limite da subtração é a subtração dos limites),
Passo 2
Substituindo os limites, temos
Não escreve essa última igualdade na prova, seu professor não vai curtir muito, fiz isso só pra tu ver que o numerador é não nulo enquanto o denominador é. Ou seja, nossas contas estão indo para infinito. Resta-nos saber se ou .
Vamos analisar se o limite será ou .
Perceba que estamos nos aproximando de pela esquerda, ou seja, valores menores que ele. Sendo assim, nosso denominador tende a ficar negativo, já que estamos tirando um de um número menor, o que significa dizer que teremos:
Sendo assim,
Passo 3
Agora vamos ver como a função se comporta à direita a desse ponto, isto é,
Usando as mesmas regras, na mesma ordem que fizemos anteriormente,
Perceba que agora estamos nos aproximando de pela direita, ou seja, valores maiores que ele. Sendo assim, nosso denominador tende a ficar positivo, já que estamos tirando um de um número maior, o que significa dizer que teremos:
Daí,
Passo 2
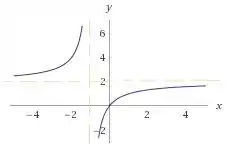
Logo, temos uma assíntota , na qual a função explode positivamente à direita deste ponto e à esquerda, o qual pode ser visto conforme o gráfico:
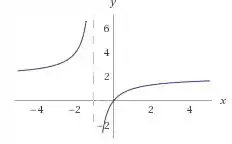
Passo 3
Olhe novamente para a função, olhou? Viu que temos um polinomio não constatnte dessa ves? Então podemos tentar encontrar assíntotas horizontais, para isso, devemos tender a e.
Vamos começar por . Ou seja, vamos calcular
.
Vamos usar a regra para limites no infinito de funções racionais, ou seja, dividir o numerador e o denominador pelo termo de x de maior potencia. Neste caso será o próprio x,
Usando as mesmas regras, na mesma ordem que fizemos anteriormente,
Da mesma forma,
Logo, temos uma assíntota horizontal , ou seja,
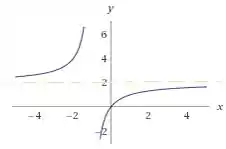
Resposta