Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.4 - Ex. 32
Faça o gráfico do ramo superior da hipérbole
Passo 1
Como já nos foi informado, a equação dada consiste na de uma hipérbole. Esta equação já está na sua forma reduzida, e, como o valor que multiplica é um número positivo, o eixo que contém os focos da hipérbole é o eixo Y. Para obtermos a equação do ramo superior, basta encontrar os pontos tais que .
Passo 2
Vamos inicialmente resolver a equação da hipérbole em função de .
Passo 3
Como pode ser observado, obtemos duas soluções de valor igual e sinal trocado. A grande questão é: qual o sinal que identifica o ramo superior da hipérbole? Para isto, basta descobrirmos qual equação nos fornece . Como o resultado de uma raiz é sempre maior ou igual a , a equação do ramo superior será:
Passo 4
Agora, basta obter o gráfico da função
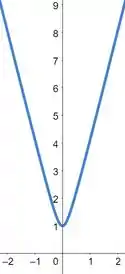
Resposta
