Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 18

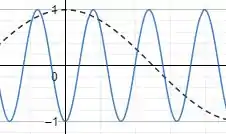
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função?

- c o s   ( 2 π x )

Passo 1

Então galera, para os exercícios 13-22 precisamos relembrar aqui algumas fórmulas para mudança de escala vertical e horizontal e para reflexão também, tudo bem? Se liga!

Assim como discutido na seção 2 do George, temos que:

y = c f x   a l o n g a   v e r t i c a l m e n t e

y =   1 c f x   c o m p r i m e   v e r t i c a l m e n t e

y = f c x   c o m p r i m e   h o r i z o n t a l m e n t e

y = f 1 c x   a l o n g a   h o r i z o n t a l m e n t e

y =   - f x r e f l e t e   e m   t o r n o   d e   x

y = f - x   r e f l e t e   e m   t o r n o   d e   y

Passo 2

Facilmente notamos que a função que nos foi dada apresenta 1 mudança de escala do tipo:

y = f c x

No qual isso implica em uma compressão horizontal. Ademais, a função que nos foi dada também apresenta uma reflexão do tipo:

y =   - f x

No qual isso implifica em uma reflexão em torno do eixo x . Sabendo dessas informações, temos que nosso gráfico ficará assim:

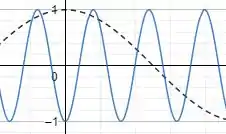
No qual a função pontilhada é c o s   x e afunção azul é - c o s   ( 2 π x ) .

Passo 3

Por fim devemos descobrir o período da função que nos foi dada. Para calcularmos o período é beeem tranquilão! O período é dado pela razão:

P =   2 π | k |

No qual k é o número que acompanha a variável x na função. No nosso caso k = 2 π , logo:

P =   2 π 2 π

∴ P =   1

Resposta

P = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito elétrico tem uma força eletromotriz de 100 sen ⁡ 200 t volts em t s e um resistor de 10 ohms, além de um indutor de 0,1 henry ligado em série. (b) Dê um valor aproximado de i para valores
Um circuito elétrico tem uma força eletromotriz de 100 sen ⁡ 200 t volts em t s e um resistor de 10 ohms, além de um indutor de 0,1 henry ligado em série.Se a corrente for i ampères em t s e i = 0 , q
Um circuito elétrico tem uma força eletromotriz de 10 sen ⁡ 10 t volts em t s e um resistor de 3 ohms, além de um indutor de 1 henry ligado em série. Se a corrente for i ampères em t s e i = 0 , quand
Nos Exercícios 1 e 2, ache a medidade equivalente em radianos.1. a) 60°; b) 135°; c) 210°; d) -150°; e) 20°; f) 450°; g) -75°; h) 100°
Nos Exercícios 5 a 12, determine o valor exato da função.6. a) cos ⁡ π 3 ; b) sen ⁡ π 4 ; c) cos ⁡ - π 2 ; d) sen ⁡ ( - 2 π ) ;