Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 24
Faça os gráficos das funções nos Exercícios 23-26 no plano (eixo horizontal, eixo vertical). Qual é o período de cada função? Que simetrias os gráficos possuem?
24.
Passo 1
Se aproximarmos o de a tangente fica pequena muito rapidamente, mas como tem um sinal negativo na frente dela a função vai tender ao infinito.
Quando .
Se aproximarmos o de a tangente fica grande muito rapidamente, mas como tem um sinal negativo na frente dela a função vai tender à menos infinito
.A partir dai as coisas começam a se repetir:
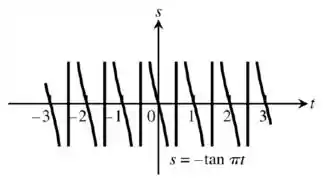
Como podemos observar no gráfico o período é de
E o gráfico possui uma simetria na origem.
Resposta
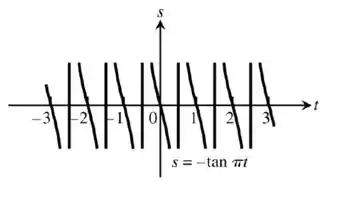
Simetria na origem.
Exercícios de Livros Relacionados
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o t g t = - 1 está satisfeita.
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g 11 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o t g t = 0 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e n( t ) = 1 está satisfeita.
Encontre todos os valores de t no intervalo 0,2 π em que a equaçãot g t = - 1 3 √ 3 está satisfeita.