Faça os gráficos das funções nos Exercícios 37-46. Que simetrias, se houver, possuem os gráficos? Especifiqueos intervalos dentros dos quais a função é crescente e os intervalos em que ela é decrescente.

39.

e nunca irão valer zero, quando for negativo e se aproximar de zero o começa a ficar grande muito rapidamente. Quando for positivo e se aproximar de zero o começa a ficar pequeno muito rapidamente.

E quando tender ao infinito e a menos infinito o vai se aproximar de zero, mas nunca chegar nele.

Plotando alguns pontos, temos o gráfico:

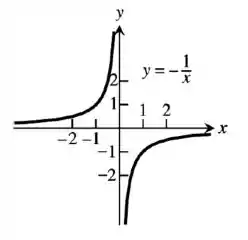
A função possui simetria na origem.

Ela é uma função crescente em todo o seu domínio: , e nunca decresce.