Faça gráficos de que revelem todos os aspectos importantes da curva. Em particular, você deve usar gráficos de para estimar os intervalos crescentes e decrescentes, valores extremos, intervalos de concavidade e pontos de inflexão.
Passo 1
Faaala meu querido, tudo certo?Nessa questão nos é dado a seguinte função:
E o enunciado pede para a gente fazer o gráfico dessa função e de suas derivadas primeira e segunda.
Então nós basicamente vamos encontrar as derivadas dessa função e colocar essas derivadas e a função em um software gráfico.
A partir dos gráficos de , e , nós vamos obter algumas informações.
Intervalos de crescimento e decrescimento:
Eles podem ser obtidos observando o gráfico da função e vendo quando que ele cresce ou decresce. Ou podem ser obtidos observando o gráfico da derivada e vendo quando ela é positiva
A função cresce e quando ela é negativa
A função decresce.
Os valores extremos podem ser obtidos observando o gráfico da função e vendo quando ele possui um máximo ou um mínimo. Ou podem ser obtidos observando o gráfico da derivada e vedno quando ela troca de sinal, o que geralmente ocorre quando
Ou quando
Sendo que quando ela troca de negativa para positiva temos um ponto de mínimo e quando ela troca de positiva para negativa temos um ponto de máximo.
Os intervalos de concavidade podem ser obtidos observando-se o gráfico da função e vendo quando ele possui concavidade para cima ou para baixo. Ou a partir do gráfico da segunda derivada , de forma que quando a segunda derivada é positiva
A função é côncava para cima e quando a segunda derivada énegativa
A função é côncava para baixo.
Por fim, os pontos de inflexão podem ser obtidos verificando o gráfico da segunda derivada quando ele troca de sinal o que geralmente ocorre quando
Ou quando
Passo 2
Bom pessoal, neste exercício nós devemos usar algum recurso para plotar gráficos e calcular valores das funções. Tendo isso, vamos ao exercício:
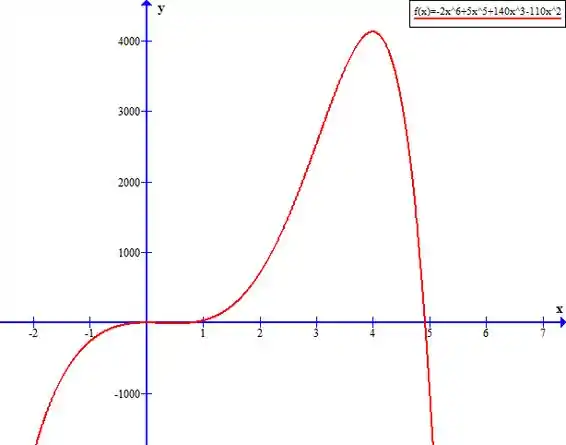
Vamos dar um ZOOM perto do zero:
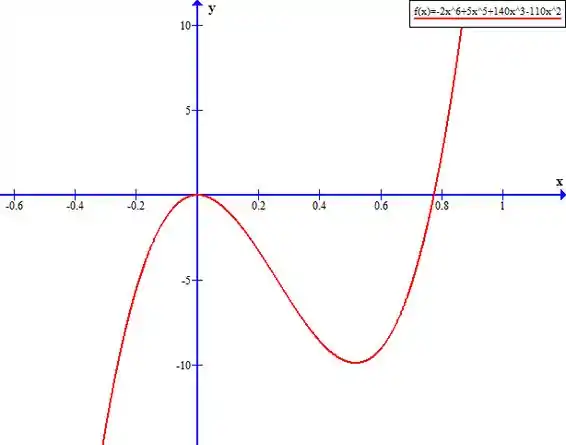
As raízes reais da função são:
Passo 3
A função é
Agora vamos para a primeira derivada:
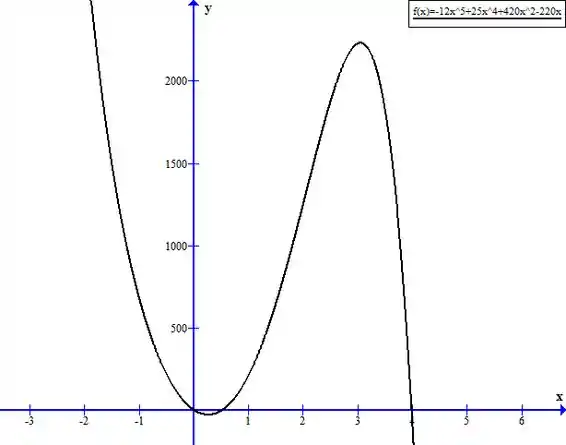
As raízes reais de são:
Para encontrar intervalos crescentes e decrescentes, temos que analisar a primeira derivada da função, onde:
Vamos usar o gráfico e a definição acima para encontrar os intervalos crescentes e decrescentes:
Crescente:
Decrescente:
Passo 4
Pontos de máximos e mínimos. Para encontrar estes pontos, temos que conhecer as raízes de e avaliar se há troca de sinal de Ou então avaliar o sinal da segunda derivada nas raízes de
Vamos então calcular a segunda derivada de
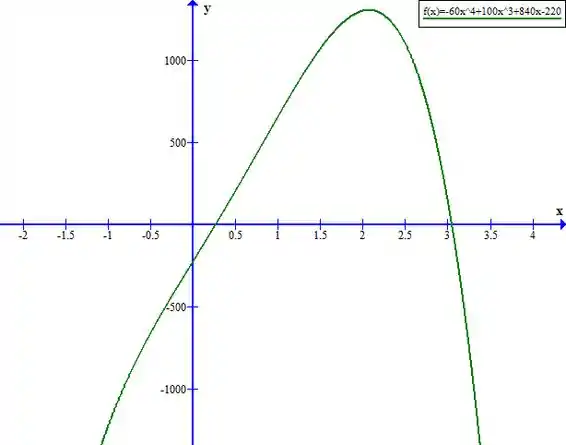
Checando então nas raízes de
(Você também pode verificar esses pontos avaliando o sinal de nas proximidades das raízes. Por exemplo, em , temos que antes desse ponto a derivada é negativa e após esse ponto a derivada é positiva, portanto esse é um ponto de mínimo.)
Passo 5
Para analisar a concavidade da função e achar seus intervalos, devemos usar a segunda derivada da função.
Pontos de inflexão ocorrem na mudança de concavidade.
Avaliando novamente o gráfico da segunda derivada temos o seguinte:
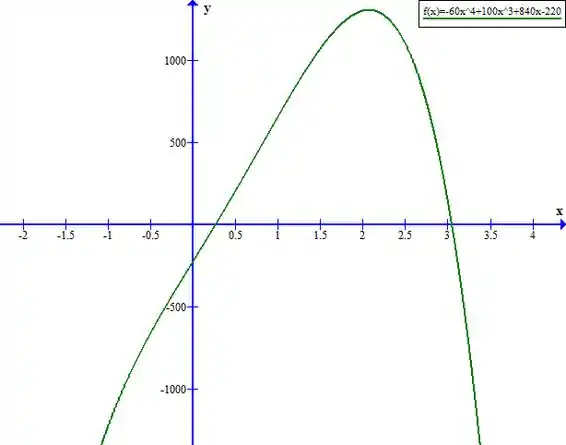
Suas raízes são:
Analisando os intervalos:
Logo, os intervalos são:
Agora vamos ver novamente o gráfico de f(x) para confirmar todos os valores encontrados:
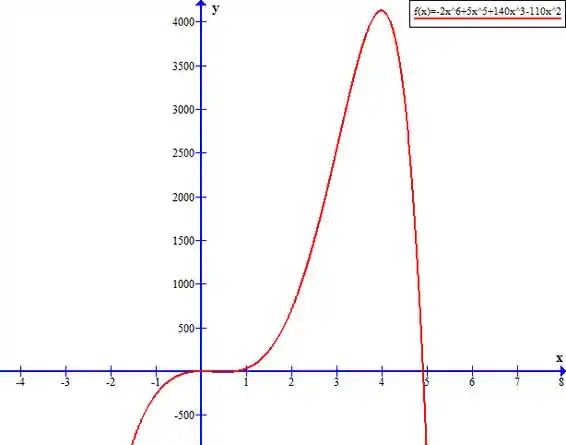
Resposta
Desenvolvimento nos Passos.