Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.5 - Ex. 4
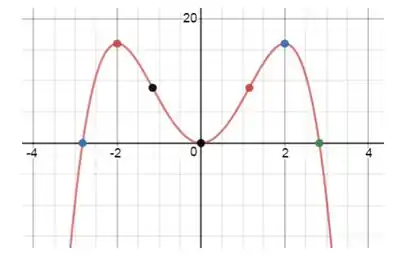
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Oiee, bora lá
Para iniciar a questão vamos relembrar um pouco da teoria:
Domínio: Conjunto de todos os valores de para os quais a função é definida.
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Simetria:
- Função Par:
- Função Ímpar:
Assíntotas:
- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.
- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Passo 2
Vamos usarmos o roteiro de esboço de curvas dado na seção para esboçar o gráfico da função dada. Precisamos achar a primeira e segunda derivada para analisar crescimento e concavidade, procurar as interseções com eixos, etc...
Como se trata de um polinômio, o domínio é real: .
Vamos achar as interseções com os eixos e . Para o ponto que corta o eixo , basta tomar , assim, .
Passo 3
Vemos então que a curva passa pela origem . Para as interseções com o eixo , fazemos , assim
Assim, as raízes são , . As interseções com os eixos são e .
Note que tem apenas expoentes pares de , assim ela é par, sendo simétrica com relação ao eixo .
Passo 4
Como se trata de um polinômio, não tem assíntotas:
Passo 5
Para estudarmos os intervalos de crescimento e decrescimento, precisamos derivar :
Desta forma,
Assim, é ponto de mínimo local e e são pontos de máximo local.
Mínimo local: ; máximo local: .
Passo 6
Para a concavidade, precisamos da segunda derivada:
Assim,
Como , os pontos são pontos de inflexão.
Resposta
Esboço da curva:
