Faça em uma mesma tela os gráficos das funções dadas. Como estão relacionados esses gráficos?
,, ,
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar na mesma tela, os gráficos das funções ,, e .
Pra isso, temos que lembrar de algumas propriedades do gráfico das funções exponenciais, do tipo , como o fato delas sempre passarem pelo ponto , já que para .
Além disso, observe que a função exponencial cresce mais rapidamente à medida que fica maior (para ).
Então, vamos plotar nossas curvas com base nisso e analisar a relação entre elas.
Vamos lá!
Passo 2
Bom, primeiro temos que plotar os gráficos na mesma tela.
Se você estiver fazendo o gráfico na mão, pode substituir por alguns valores em cada caso, pra ter uma ideia do quão rápido a função vai crescer ou decrescer, e depois só traçar, lembrando do “formato” das funções exponenciais que tem sempre a mesma característica.
No nosso caso, temos:
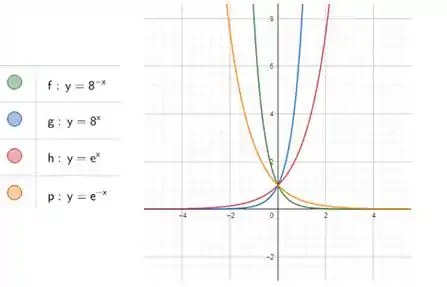
Tranquilo até aqui? 😉
Passo 3
Agora, queremos saber como os gráficos estão relacionados.
Podemos ver que todos se cruzam no ponto , certo? Isso porque sempre que , temos um número elevado a zero, que é , como vimos no passo .
Toda função exponencial, independemente da base, vai passar por esse ponto.
Vemos também que as funções e possuem a mesma inclinação, com a diferença de que a primeira é crescente, e a outra é descrescente.
O mesmo acontece com e .
Seria como se a gente pegasse a primeira e refletisse em torno do eixo para gerar a segunda!
Valeu, galera! Até a próxima! 😉
Resposta
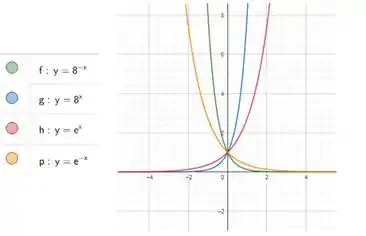
Todos as funções passam pelo ponto .
Uma função é a reflexão em torno do eixo da outra função quando os expoentes são opostos e as bases são iguais.