Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 9
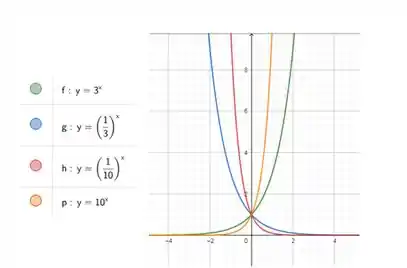
Faça em uma mesma tela os gráficos das funções dadas. Como estão relacionados esses gráficos?
, ,
Passo 1
Opa, bora lá! Precisamos desenhar em um mesmo gráfico várias curvas:
, ,
A gente também precisa entender a relação entre esses gráficos!
Bom, primeiro temos que plotar os gráficos. Se você estiver fazendo o gráfico na mão, pode substituir por alguns valores em cada caso, pra ter uma ideia do quão rápido a função vai crescer.
Depois só traçar, lembrando do ‘formato’ das funções exponenciais.
Passo 2
Vamos montar uma tabelinha com esses valores e os funções calculadas:
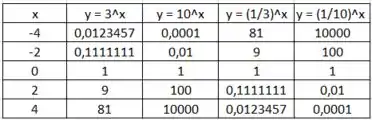
Traçando o gráfico, temos:
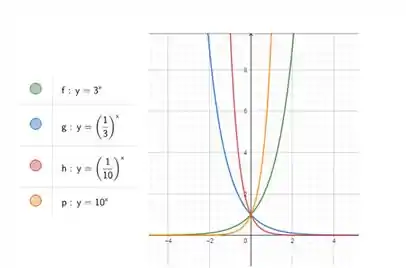
Passo 3
Depois, queremos saber como os gráficos estão relacionados.
Podemos ver que todos se cruzam no ponto , certo? Isso porque sempre que , temos um número elevado a zero, que é . Toda função exponencial, independemente da base, vai passar por esse ponto.
Vemos também que as funções e possuem a mesma inclinação, com a diferença de que a primeira é crescente, e a outra é descrescente. O mesmo acontece com e . Seria como se a gente pegasse a primeira e refletisse ao redor do eixo para gerar a segunda!
Aqui podemos ver que
Ou seja, elevar um número a é o mesmo que elevar o seu oposto a .
Prontinho!
Resposta
Todos as funções passam pelo ponto . Uma função é a reflexão em torno do eixo da outra função quando as bases são números inversos e os expoentes são iguais.
