Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.3 - Ex. 11

Faça o seguinte:

Estabeleça uma integral para o comprimento da curva.

Trace a curva para ver como ela é

Use seu programa gráfico ou programa para calcular integrais e determine o comprimento da curva numericamente.

Passo 1

Letra

Para calcularmos o comprimento da curva, devemos usar a fórmula para o comprimento.

Como temos uma função de , a fórmula vai ser:

Entao precisamos de duas coisas, o intervalo de intergração, que ele deu no enunciado, e a derivada da , que é a função do enunciado.

O intervalo é de até , vamos para a derivada.

Derivando:

Passo 2

Vamos para a interal do comprimento agora, usando oque achamos:

Ele so quer a integral mesmo, não precisamos resolver não.

Passo 3

Letra

Jogando a função num programa de fazer gráfico, vamos ter:

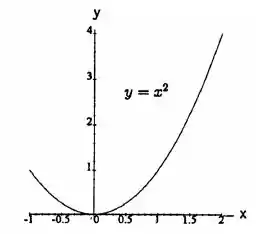
Essa é a curva que ele pediu.

Passo 4

Letra

Jogando essa integral num programa, para resolver numericamente, vamos encontrar:

Resposta

Letra

Letra

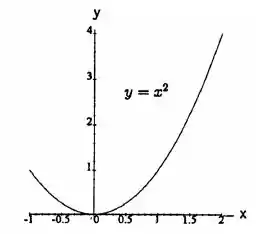
Letra

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o seguinte: a ) Estabeleça uma integral para o comprimento da curva. b ) Trace a curva para ver como ela é c ) Use seu programa gráfico ou programa para calcular integrais e determine o comprimen

Nos Exercícios 1-10, determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são.14- x = 1 - y 2 , - 1 2 ≤ y ≤ 1 2

Enuncie uma fórmula integral para encontrar o comprimento de arco de uma curva lisa y = f ( x ) acima de um intervalo [ a ,b ] e use somas de Riemann para derivar a fórmula dada.

Seja C a curva y = e x entre x = 0 e x = ln ⁡ 10 . Em cada parte, monte, mas não calcule, uma integral que resolva o problema.(a) Encontre o comprimento de arco de C integrando em relação a x .(b) Enc

Encontre o comprimento de arco no segundo quadrante da curva x 2 3 + y 2 3 = 4 de x = - 8 a x = - 1 .