Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.7 - Ex. 8

A face da comporta de uma barragem é vertical e tem a forma de um trapézio isósceles com 3 m no topo, 4 m na base e 3 m de altura. Se a base superior está a 20 m abaixo da superfície da água, ache a força total devido à pressão da água sobre a comporta.

Passo 1

Se temos uma face submersa verticalmente em um líquido de densidade ρ , e o comprimento da face a uma profundidade de x unidades puder ser representado por uma função f ( x ) , contínua e positiva no intervalo [ a ,   b ] , então a força causada pela pressão líquida na face é:

F = ρ g ∫ a b x f x d x   N

Devemos primeiro achar uma função f ( x ) que descreva o comprimento da parede em função da profundidade x da água, para podermos calcular F usando a fórmula.

Passo 2

Queremos a largura f ( x ) numa profundidade x da água. A figura abaixo mostra que podemos encontrá-la por semelhança de triângulos. A medida d é igual a f x - 3 2 = 0,5 f x - 1,5

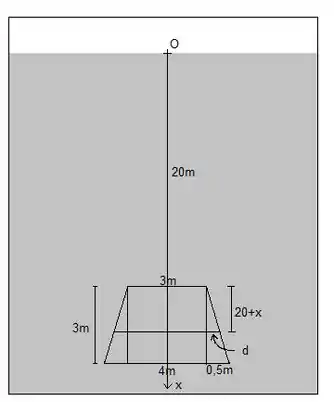
Temos então, por semelhança de triângulos:

0,5 f x - 1,5 x - 20 = 0,5 3 = 1 6 ⇒ 0,5 f x - 1,5 = x - 20 6 ⇒ f x - 3 = x - 20 3

⇒ f x = x - 20 3 + 3 = x - 11 3

Passo 3

Aplicando então a fórmula, com f x = x - 11 3 e x ∈ 20 ,   23   m:

F = ρ g ∫ 20 23 x ⋅ x - 11 3 d x = 1 3 ρ g ∫ 20 23 x 2 - 11 x d x

= 1 3 ρ g x 3 3 - 11 x 2 2 20 23 = 1 3 ρ g 23 3 3 - 11 ⋅ 23 2 2 - 20 3 3 - 11 ⋅ 20 2 2

= 1 3 ρ g ⋅ 12167 3 - 5819 2 - 8000 3 + 2200 = 1 3 ρ g ⋅ 679,5 = 226,5 ρ g

Para ρ = 1000   k g / m 3 e g = 9,81   m / s 2 :

F = 2221965   N

Resposta

F = 2221965   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

OS extremos de uma tina são triângulos equiláteros com lados que medem 60 cm. Se a agua na tina estiver 30 cm de profundidade, ache a força devido À pressão do liquido em um extremo Resolva usando F =
Um tanque retangular cheio de água tem 60 cm de largura e 46 cm de profundidade. Ache a força decorrente da pressão do líquido sobre um extremo do tanque.
Resolva o exercício 2, se o centro da placa estiver a 1 m abaixo da superfície. (Veja o exercício 2).
Os extremos de uma tina são triângulos equiláteros com lados que medem 60 cm. Se a água na tina tiver 30 cm de profundidade, ache a força devido à pressão do líquido em um extremo.
Uma placa retangular é submersa verticalmente em um tanque, de forma que o lado de cima esteja na superfície da água. Se o comprimento da placa for de 10 cm e a profundidade for de 8 cm, ache a força