Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 3
Ache o volume do solido gerado por rotação, em torno do eixo x da região limitada pela curva y =, a reta x= e eixo x.
Passo 1
Desenhando o problema
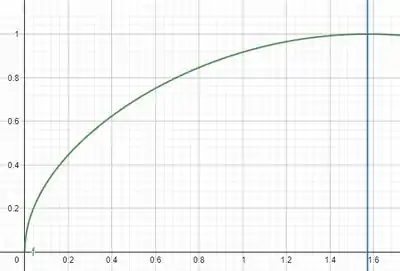
No plano XY o solido tem essa forma. Com a curva verde a função e a azul x =
Como é um solido de revolução. Então o seu volume é
Passo 2
No nosso caso o limite de integração é entre [ ,0]
Logo : V =
V =
V =
Resposta
V =
Exercícios de Livros Relacionados
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = x 2 + 1 y = x + 3
33. Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região do exercício 32.
32. Ache o volume do sólido gerado pela rotação, em torno do eixo y , da região limitada pela reta que passa por (1,3) e (3, 7) e pelas retas y = 3 , y = 7 e x = 0.
Ache o volume do sólido gerado pela rotação da região abaixo (região do exercício 34) em torno do eixo y .
Ache o volume do sólido gerado pela rotação da região à direita do eixo y , limitada pela curva y = x 9 - x 2 4 e pelo eixo x , em torno do eixo x .