Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 66
Um fazendeiro deseja caminhar a uma taxa constante de seu estábulo até um rio reto, encher um balde e levar para casa no menor tempo.
a) Explique como esse problema se relaciona com o princípio de Fermat e o problema da reflexão da luz do Exercício 64.
b) Use o resultado do Exercício 64 para descrever geometricamente qual o melhor caminho para o fazendeiro seguir.
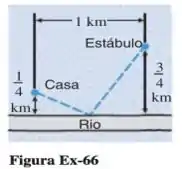
c) Use a parte b) para determinar onde o fazendeiro deverá encher o balde se a casa e o estábulo estiverem localizados como na Figura Ex-66.
Passo 1
a) Então galera, o Exercício 64 é exatamente o mesmo problema e exatamente a mesma situação que temos aqui. A única diferença dos problemas é que a fonte que está se movendo é o fazendeiro (nesse problema), enquanto no problema 64 a fonte que estava se movendo era a luz. Podemos esboçar esse problema da seguinte forma:
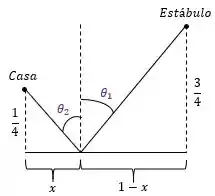
Note que a única diferença desse exercício para o 64 são os valores da altura e da largura do caminho, mas isso não interefere em nada no resultado final. Aqui o princípio de Fermat continua valendo:
Passo 2
b) Do exercício 64 chegamos na seguinte conclusão:
Que implica em:
Sendo assim, podemos concluir que, geometricamente, o melhor caminho que o fazendeiro poderia tomar seria o caminho que satisfaz a relação acima!
Passo 3
c) Então galera, na demonstração da Lei de Snell (Passo 2), chegamos na seguinte relação:
No nosso caso, temos que e . Ademais, temos que . Substituindo esses valores:
Logo:
E essa é a nossa resolução, galera! 😉
Resposta
Ei, a resposta está no passo a passo :)