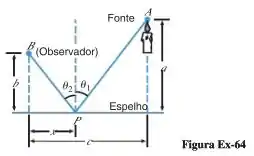
O Princípio de Fermat (biografia à página 275) na óptica afirma que a luz, viajando de um ponto para outro, segue aquele caminho para o qual o tempo total no percurso é mínimo. Em um meio uniforme, os caminhos de “tempo mínimo” e de “menor distância” vêm a ser iguais; assim, a luz se não obstruída, viaja em linha reta. Suponha que tenhamos uma fonte de luz, um espelho plano e um observador em um meio uniforme. Se um raio de luz deixa a fonte, bate em um espelho e vai até o observador, então sua trajetória consiste em dois segmentos de reta, conforme mostra a Figura Ex-64. De acordo com o princípio de Fermat, a trajetória é tal que o tempo gasto no percurso é mínimo ou, como o meio é uniforme, a trajetória será tal que a distância total percorrida de a a será a menor possível. Supondo que o mínimo ocorre quando , mostre que o raio de luz irá atingir o espelho em um ponto , tal que o “ângulo de incidência” será igual ao “ângulo de reflexão” .

Olhando para o triângulo retângulo da direita na figura do enunciado, temos o seguinte:

E olhando para o triângulo retângulo da esquerda, teremos:

Logo, nossa expressão será:

E essa é a nossa expressão para o tempo gasto no percurso. Como o mínimo ocorre quando , então:

Igualando a zero:

E para isso dar zero:

Show!

Então galera, no passo anterior chegamos em uma igualdade muito interessante! Se observarmos bem, o lado esquerdo da equação é o seguinte:

Já o lado direito da equação é o seguinte:

Se substituirmos esses resultados, teremos:

Que implica em:

Como queríamos demonstrar!

E essa é a nossa prova, galera! 😉