Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 4c
Fazer o gráfico das funções seguintes e determinar os respectivos limites. Para melhor visualização, traçar, também, o gráfico das retas indicadas. A seguir, determinar analiticamente os limites dados e comparar os resultados.
Passo 1
Primeiro vamos traçar o gráfico da função, já com a reta marcada.
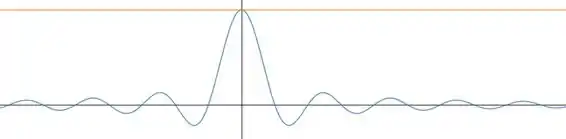
Beleza, então visualmente já conseguimos determinar que:
E pra valores de maiores, ela tá cada vez mais tendendo pra .
Passo 2
Vamos confirmar com as contas. O primeiro limite que a gente viu é quase o limite fundamental, mas com um detalhe diferente. Vamos tentar forçar aparecer o limite fundamental pra calcular.
Esse é o fundamental!
Pros outros, com tendendo ao infinito, o que a gente tem é uma função limitada (), que só vai de a , sendo dividida por um valor enorme! Esses dois limites tendem pra . Confirmado!