Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 69
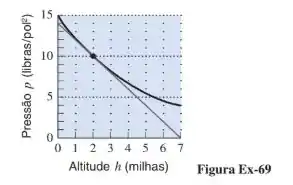
A figura abaixo mostra o gráfico da pressão atmosférica (libras/pol²) versus a altitude (milhas) acima do nível do mar.
- A partir do gráfico e da reta tangente em mostrados no gráfico, estime os valores de e a uma altitude de milhas.
- Se a altitude de um veículo espacial aumentar a uma taxa de quando ele está a 2 milhas acima do ar, com que rapidez a pressão irá variar em relação ao tempo neste instante?
Passo 1
Foi dado um gráfico da pressão em função da altura . Esse gráfico é uma curva que passa pelo ponto . Também foi nos dado a reta tangente ao gráfico em .
Passo 2
- Observando o gráfico, vemos que quando .
- Queremos descobrir a variação de em relação ao tempo, ou seja, . Note que nós tempos e (que é a velocidade de ). Podemos relacionar tais grandezas a partir da regra da cadeia. Veja:
Para obter o valor de , devemos olhar para a inclinação da reta tangente ao gráfico de no ponto . Observe que a reta tangente passa pelos pontos e . Sendo assim, o coeficiente angular será:
Sendo assim, temos que
Passo 3
Resposta
- .
- .
Exercícios de Livros Relacionados
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = e 2 x / 3
Determine as derivadas das funções y = 3 - t
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = e - 5 x
Aceleração constante. Suponha que a velocidade de um corpo em queda seja v = k s m/s (com k uma constante) no instante em que o corpo caiu s metros do ponto de partida. Mostre que a aceleração do corp
Determine a tangente à curva y = 2 ⋅ t g ( π x / 4 ) em x = 1 Coeficiente angulares de uma curva tangente: Qual o menor valor de coeficiente angular que a curva pode ter no intervalo - 2x2 ? Justifiqu