Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 73

Seja

f x = x sin ⁡ 1 x ,   x ≠ 0 0 ,   x = 0

  1. Mostre que f é contínua em x = 0 .
  2. Use a definição 2.2.1 para mostrar que f ' 0 não existe.
  3. Encontre f ' x para x ≠ 0 .
  4. Determine se lim x → 0 ⁡ f ' x existe.

Passo 1

Esse é um exercício bem complexo que possui vários passos. Então, não se preocupe se ficar um pouco perdido no meio de tantas contas! Respire e leia de novo, quantas vezes por preciso, okay?

Passo 2

  1. Vamos começar mostrando que f é contínua em x = 0 . Porém, como mostramos que uma função é contínua em um determinado ponto x = p ? A resposta é o seguinte: calculamos lim x → p ⁡ f x . Se o valor desse limite for igual f p , então f será contínua em x = p . Ou seja,

    2. lim x → p ⁡ f x = f p ⟺ f   é   c o n t í n u a   e m   x = p

    Queremos mostrar que f é contínua em x = 0 . Logo, devemos mostrar que

    lim x → 0 ⁡ f x = f 0 = 0

    Vamos então calcular esse limite!

    lim x → 0 ⁡ f x = lim x → 0 ⁡ x sin ⁡ 1 x

    Notemos o seguinte: a função seno é sempre limitada entre - 1 e 1 . Sendo assim,

    - 1 ≤ sin ⁡ 1 x ≤ 1

    Multiplicando tudo por x > 0 , temos:

    - x ≤ x sin ⁡ 1 x ≤ x

    Note que lim x → 0 ⁡ - x = 0 e lim x → 0 ⁡ x = 0 . Ou seja, pelo teorema do confronto, temos que

    lim x → 0 ⁡ x sin ⁡ 1 x = 0

    Ou seja,

    lim x → 0 ⁡ f x = f 0

    o que mostra que f é contínua em x = 0 .

    Passo 3

  2. Pela definição, temos que

    3. f ' 0 = lim x → 0 ⁡ f x - f 0 x - 0 f ' 0 = lim x → 0 ⁡ x sin ⁡ 1 x - 0 x f ' 0 = lim x → 0 ⁡ sin ⁡ 1 x

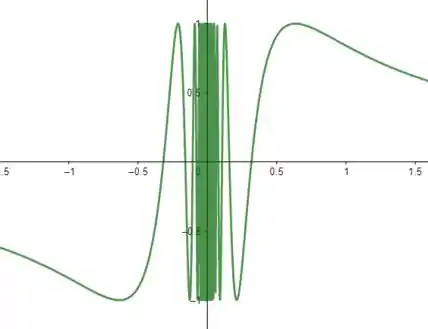
    Porém, esse último limite não existe! Para você enxergar isso, note que sin ⁡ 1 x é uma função periódica que fica oscilando “loucamente” entre - 1 e 1 quando x vai se aproximando de 0 , como mostra o gráfico abaixo. Assim, como a função sin ⁡ 1 / x não se aproxima de nenhum valor quando x → 0 , então f ' 0 não existe.

    Passo 4

  3. Para x ≠ 0 calculamos a derivada normalmente!

    4. f ' x = d d x x sin ⁡ 1 x

    Primeiro, devemos aplicar a regra do produto:

    f ' x = d d x x sin ⁡ 1 x + x d d x sin ⁡ 1 x f ' x = 1 ⋅ sin ⁡ 1 x + x d d x sin ⁡ 1 x

    Para calcular d d x sin ⁡ 1 x , usamos a regra da cadeia. Seja u = 1 / x . Assim,

    d d x sin ⁡ 1 x = d d u sin ⁡ u d u d x d d x sin ⁡ 1 x = cos ⁡ u - 1 x 2 d d x sin ⁡ 1 x = - 1 x 2 cos ⁡ 1 x

    Logo,

    f ' x = sin ⁡ 1 x - 1 x cos ⁡ 1 x

    Passo 5

  4. Notemos que lim x → 0 ⁡ f ' x pois teríamos que calcular lim x → 0 ⁡ sin ⁡ 1 x , e já vimos que tal limite não existe.

Resposta

  1. Demonstração.
  2. Demonstração.
  3. f ' x = sin ⁡ 1 x - 1 x cos ⁡ 1 x .
  4. Não existe.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aceleração de uma partícula. Uma partícula se desloca ao longo do eixo x com velocidade d x / d t = f ( x ) . Mostre que sua aceleração é f x f ' ( x ) .
Meteorito em queda. Quando um meteorito pesado está a s quilômetros do centro da Terra sua velocidade de entrada na atmosfera é inversamente proporcional a s . Mostre que a aceleração do meteorito é i
Derivada de s e n( 2 x ) . Represente graficamente a função y = 2 cos ⁡ 2 x para - 2 ≤ x ≤ 3.5 . Depois, na mesma tela, faça o gráfico de y = s e n 2 x + 2 h - s e n ( 2 x ) h Para h = 1.0 ; 0.5 e0.2
Usando a regra da cadeia, mostre que a regra da potência d d x x n = n x - 1 vale para as funções x n x 1 / 4 = x
Usando a regra da cadeia, mostre que a regra da potência d d x x n = n x - 1 vale para as funções x n x 3 / 4 = x x