Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 70

A força F (quilogramas) agindo em um ângulo θ com a horizontal necessária para arrastar, ao longo da superfície horizontal a uma velocidade constante, um caixote que pesa W quilos é dada por

F = μ W cos ⁡ θ + μ sin ⁡ θ

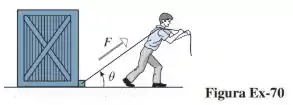
onde μ é uma constante denominada de atrito de escorregamento entre o caixote e a superfície (ver figura a seguir). Suponha o caixote com 70   k g e μ = 0,3 .

  1. Encontre d F / d θ quando θ = 30 ° . Expresse sua resposta em k g / g r a u .
  2. Encontre d F / d t quando θ = 30 ° e θ está diminuindo a uma taxa de 0,5 ° / s nesse instante.

Passo 1

Foi nos dado uma expressão

F = μ W cos ⁡ θ + μ sin ⁡ θ

Com W = 70   k g e μ = 0,3 . O ângulo θ é variável, de modo que podemos tratar F como sendo uma função exclusiva de θ .

Passo 2

  1. Note que podemos escrever F da seguinte maneira:

    2. F = μ W cos ⁡ θ + μ sin ⁡ θ - 1

    Sendo u = cos ⁡ θ + μ sin ⁡ θ , temos:

    F = μ W u - 1

    Assim, aplicando a regra da cadeia:

    d F d θ = d F d u d u d θ d F d θ = - μ W u - 2   - sin ⁡ θ + μ cos ⁡ θ d F d θ = - μ W - sin ⁡ θ + μ cos ⁡ θ cos ⁡ θ + μ sin ⁡ θ 2

    Substituindo os dados numéricos, temos

    d F d θ = - 0,3 × 70 - sin ⁡ 30 ° + 0,3 cos ⁡ 30 ° cos ⁡ 30 ° + 0,3 sin ⁡ 30 ° 2 d F d θ = - 15,45   k g / g r a u

    Passo 3

  2. Queremos calcular o valor de d F / d t . Porém, temos apenas os valores de d F / d θ e de d θ / d t . Como poderemos, portanto, calcular d F / d t ? A resposta está na regra da cadeia. Veja que:

d F d t = d F d θ ⋅ d θ d t d F d t = - 15,45 0,5 d F d t = - 7,725   k g / s

Resposta

  1. - 15,45   k g / g r a u .
  2. d F d t = - 7,725   k g / s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Temperaturas em Fairbanks, Alaska. O gráfico a seguir mostra a temperatura média em Fahrenheit em Fairbanks, Alaska, durante um ano típico de 365 dias. A equação que fornece a temperatura aproximada n
22-Calcule varphi^' (varphi (x)) sendo varphi dada por:a)varphi (x) = s e n ( x ) b)varphi (x) = (1)/(x) c)varphi (x) = l n (x^2 + 1) d)varphi (x) = e^(x^2)
21-Seja varphi a função dada por varphi (x) = x^2 + 1 . Calcule:A)varphi ' ( varphi (x) ) B)(varphi (varphi (x)))^'
20- Suponha f : R → R derivável e considere a função dada por y = x 2 f x 2 + 1 . Verifique que d y d x = 2 x . f x 2 + 1 + 2 x 3 f ' ( x 2 + 1 ) Expresse d y d x│ x = 1 │ em termos de f 2ef ' ( 2 )
17- Considere as funções dadas por y = a x 2 e y = - x 2 + 1 . Determine a para que os gráficos se interceptem ortogonalmente. (Os gráficos interceptam ortogonalmente em ( x 0 , y 0 ) se as retas tang