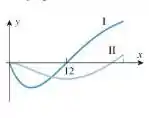
A figura abaixo mostra os gráficos de e de . Determine de qual função são os gráficos e explique seu raciocínio.

Cara, se uma função é a integral da outra, isso quer dizer que a outra é a derivada da uma, ou seja, é a derivada de . Se você não acredita em mim:

Pelo Teorema Fundamental do Cálculo:

Então, temos que achar qual a função no gráfico é a derivada.

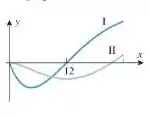
Vamos supor que a é a derivada da :

Quando a decresce (até , mais ou menos), a é negativa.

Em , a teria que ter derivada zero, já que a é zero.

A partir de , a começa a crescer e a fica positiva, como esperado da derivada da .

Como todas as nossas expectativas bateram, podemos concluir que a é a derivada da . E, portanto, é da e a é da .