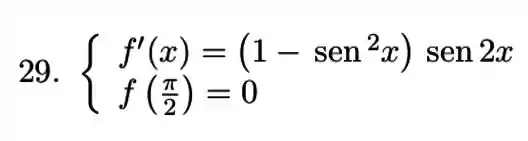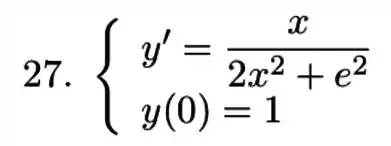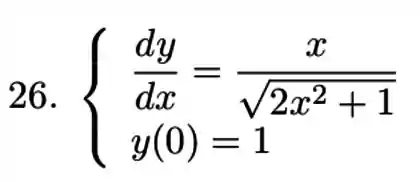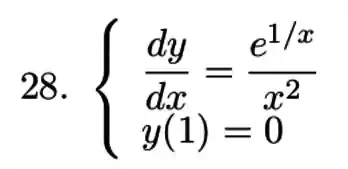Exercícios de Integrais e Problema de Valor Inicial - Lista de Exercícios Resolvida

Resolva o problema de valor inicial:

Resolva o problema:

Em um tanque CSTR, uma reação de segunda ordem ocorre segundo a lei

Sendo e substratos dessa reação. Sabe-se que é uma constante de reação e que se relacionam com a conversão de da seguinte forma:

Onde é a concentração inicial de e é a conversão de . Ache uma expressão para sabendo que

Um tanque com água está enchendo a uma taxa de:

Em litros/minuto. Determine a expressão do volume de água no tanque se litros.

Resolva o problema de valor inicial:

2b) Determine a função que cumpre:

Use o item (i) do exercício 7 para resolver a equação diferencial com a condição inicial .

Seja f uma função integrável fixada. Mostre que é uma solução para a equação diferencial com condição inicial .

Considere a função . Utilize o gráfico de f para calcular as integrais abaixo.

b)

Considere a função . Utilize o gráfico de f para calcular as integrais abaixo.

d)

Q02) Considere o seguinte PVI (Problema de Valor Inicial):

1. Mostre que a função não é solução do PVI. Neste item não é necessário resolver o PVI
2. Determine o coeficiente angular da reta tangente ao gráfico da solução do PVI em
3. Resolva o PVI

Considere a função . Utilize o gráfico de f para calcular as integrais abaixo.

Considere a função . Utilize o gráfico de f para calcular as integrais abaixo.

c)

Encontre a solução geral e a solução do problema de valor inicial para cada uma das equações abaixo:

, com a condição inicial

Encontre a solução geral e a solução do problema de valor inicial para cada uma das equações abaixo:

, com a condição inicial .

Seja uma função tal que para todo . Sabendo que é um ponto de máximo local do gráfico da função , determine:

1. A expressão de (a derivada de )
2. A expressão da função

Utilize o exercício anterior para concluir que se um objeto possui função velocidade e posição inicial , então sua função posição é dada por .

Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.

(a) Toda função é integrável.

(b) Toda função limitada é integrável.

(c) Se f é contínua em [a; b], então f é integrável em [a; b].

(d) Se f é contínua por partes em [a; b], então f é integrável em [a; b].

(e) Como o resultado de uma integral é uma área, então o resultado de uma integral sempre é maior ou igual a 0.

Considere o PVI (Problema de Valor Inicial) dado por:

1. Determine o coeficiente angular da reta tangente ao gráfico da solução do PVI em . Dica: Neste item não é necessário resolver o PVI.
2. Encontre uma função real tal que seja solução do PVI