Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.8 - Ex. 17
A figura abaixo mostra uma piscina retangular cujo fundo é um plano inclinado. Encontre a força da água sobre o fundo quando a piscina estiver cheia até o topo.
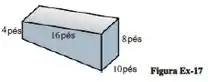
Passo 1
Para resolvermos esse problema vamos começar encontrando a dimensão do fundo pelo teorema do tio Pitagoras:
Como vemos pela figura, a piscina é meio “irregular”, é como se tivéssemos um retângulo mais um triangulo na estrutura, portanto montamos o seguinte diagrama:
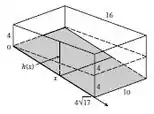
Passo 2
A partir da analise da formula 8 que fizemos no problema 16, e através da figura, vemos que a altura varia de forma que:
e...
Logo, o ângulo será:
Assim, podemos aplicar na fórmula 8:
Resolvendo a integral, temos:
Prontinho!!
Resposta
Exercícios de Livros Relacionados
23. Obtenha ∫ 1 5 f x d x se ∫ 0 1 f x d x = - 2 e ∫ 0 5 f x d x = 1
25-28. Use o Teorema 5.5 . 4 e fórmulas apropriadas de Geometria para calcular as integrais. 26 . ∫ - 2 2 1 - 3 x d x
19. Use as áreas mostradas nas figuras para encontrar(a) ∫ a b f x d x (b) ∫ b c f x d x (c) ∫ a c f x d x (d) ∫ a d f x d x
19. Use as áreas mostradas nas figuras para encontrar(a) ∫ a b f x d x (b) ∫ b c f x d x (c) ∫ a c f x d x (d) ∫ a d f x d x
25-28. Use o Teorema 5.5 . 4 e fórmulas apropriadas de Geometria para calcular as integrais. 28 . ∫ - 3 0 2 + 9 - x 2 d x