25-28. Use o Teorema e fórmulas apropriadas de Geometria para calcular as integrais.

Vamos começar quebrando essa integral.

Então precisaremos desenhar o gráfico de destacando o intervalo de e .

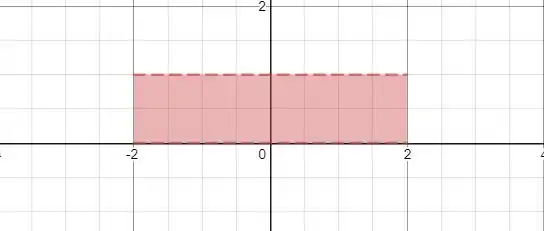
E teremos que calcular essa área, essa figura é um retângulo.

A base vai de até , então tem comprimento igual

E a altura vai de até , então tem comprimento igual a .

A área do retângulo é dada por , então .

Agora vamos deixar para o passo 3, o cálculo da integral:

Agora precisamos desenhar o gráfico de , destacando o intervalo de a .

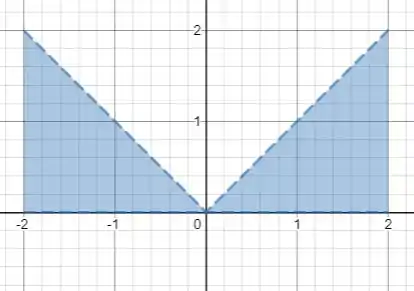
Temos que calcular a área dois triângulos em azul, porém eles são iguais, então só precisamos calcular a área de um e multiplicar por 2

A área do triângulo retângulo é dada pelo produto dos catetos.

O primeiro cateto vai de até , então tem comprimento igual a .

O segundo cateto vai de até , então tem comprimento igual a .

Então voltando para a integral.

Então resumindo, temos que:

E voltando para a integral inicial, temos: