Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 20
19. Use as áreas mostradas nas figuras para encontrar
(a)
(b)
(c)
(d)
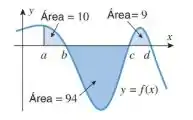
Passo 1
Vamos começar olhando as áreas e concluindo coisas sobre as integrais.
A área do gráfico de até é igual . Então, podemos afirmar:
A área do gráfico de até é igual , porém a área com sinal é de , portanto:
E para terminar essa análise inicial, temos que:
A área do gráfico de até é igual . Então, podemos afirmar:
Passo 2
Depois de termos feito essa análise, nós vamos fazer as questões.
Letra a)
Nos já calculamos esse valor diretamente pela área do gráfico, da uma olhada lá no passo 1.
Agora letra b)
Assim como aconteceu na letra a), já calculamos esse valor diretamente pela área do gráfico.
Passo 3
Vamos para a letra c)
Se você olhar lá no passo 1, não calculamos diretamente essa integral, então precisamos ajeitar isso aí.
Utilizando essa propriedade daqui de baixo:
E esses valores nos temos calculados!!
Então substituindo:
Para finalizar vamos para a letra d)
Se você olhar, assim como aconteceu com a letra c), não calculamos esse valor direto, então teremos que arrumar um jeitinho conseguirmos fazer essa questão!!!
Utilizamos essa propriedade aqui:
Porém, já calculamos:
Substituindo:
Resposta
(a)
(b)
(c)
(d)