Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 40
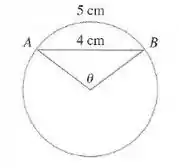
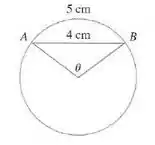
Na figura, o comprimento da corda é cm, e o comprimento do arco é cm. Encontre o ângulo central , em radianos, correto até a quarta casa decimal. Dê então a resposta com precisão de um grau.
Passo 1
E aí, galerinha! 😊
Nesse problema temos uma figura cujo comprimento da corda é cm, e o comprimento do arco é cm. A partir daí temos que encontrar o ângulo central , em radianos, correto até a quarta casa decimal usando o método de Newton.
Parece complicado?
O método de Newton é dado pela formulinha
E ele consiste em fazer cálculos em ciclos de até chegarmos em dois resultados iguais para uma determinada precisão a partir de um chute inicial.
Mas não nos foi dado nenhuma função ... então temos que determinar essa função a partir das relações trigonométricas que podemos fazer na imagem do problema.
Veja só!
Passo 2
Primeiro vamos usar o raio do círculo como sendo , e usando nós temos que:
Agora olhando a figura da pra ver que podemos usar a lei dos cossenos no triângulo , vamos lá então:
Podemos substituir o valor de na expressão que acabamos de achar:
Passando tudo para um lado da equação, podemos definir nossa função como
Para aplicar o método de Newton, vamos usar sua fórmula:
Para aplicar o método, precisamo de .
Pela regra da potência e pelo teorema fundamental do calculo...
Assim, montando a formulinha do método, temos
Tranquilo até aqui? 😁
Passo 3
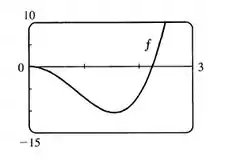
Vamos agora analisar qual valor usar para , pelo gráfico , podemos estimar .
Pronto, agora é só substituir, vai ser cansativo, mas vamos lá:
Como queremos uma precisão de quatro casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Pronto, o valor não varia mais, então paramos a interpolação.
Então o ângulo é rad .
E aí! o que achou? Responde Aí! 😁
Resposta
O ângulo é .