Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 92

Na figura existem infinitos círculos se aproximando dos vértices de um triângulo equilátero. Cada círculo toca outros círculos e lados do triângulo. Se o triângulo tiver lados de comprimento , calcule a área total ocupada pelos círculos.

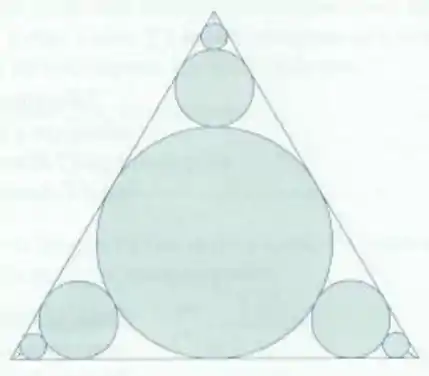
Passo 1

Galera, aqui o comando é simples, queremos a área total ocupada pelos círculos.

Podemos escrever a área total, que é a soma da área do círculo central mais vezes a soma da série de áreas dos círculos que se aproximam cada vez mais de cada vértice do triângulo:

Então vamos fazer uma figura de apenas dessa esquema, com comprimentos e ângulos, pra gente relacionar essas grandezas.

Vamos relacionar esses

Passo 2

Repare que teremos , de forma que:

Com o triângulo menor, por causa da semelhança com o triângulo , obtemos:

Veja que temos o seguinte, olhando para o segmento :

Em geral, teremos:

Passo 3

Substituindo na equação da área:

Isso é uma série geométrica e sua soma é:

Portanto:

Finalmente:

Passo 4

Show! Para termos um valor numérico da área, vamos lembrar lá da Geometria Plana qual é o raio do círculo inscrito no triângulo equilátero:

No nosso caso, , então:

Ou seja,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o número como uma razão de inteiros. 7 , 12345 -

Demonstre a parte (i) do teorema 8.

Use o comando de frações parciais em seu SCA para encontrar uma expressão conveniente para a soma parcial; então utilize essa expressão para encontrar a soma da série. Verifique sua resposta usando o

Trace as curvasy = x n ,0 ≤ x ≤ 1 , para n = 0 ,1 ,2 ,3 ,4 , … na mesma tela. Encontrando as áreas entre as curvas sucessivas, dê uma demonstração geométrica do fato, mostrado no Exemplo 6, de que ∑ n

O que está errado com o seguinte cálculo?0 = 0 + 0 + 0 + ... = (1 - 1) + (1 - 1) + (1 - 1) + ... = 1 - 1 + 1 - 1 + 1 - 1 + ... = 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + ... = 1 + 0 + 0 + 0 + ... = 1