Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 18
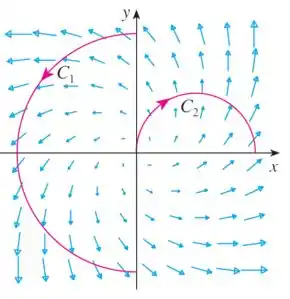
A figura mostra um campo vetorial e duas curvas e . As integrais de linha de sobre e são positivas, negativas ou zero? Explique.
Passo 1
E aii, turma, tudo certo??
Essa questão deu pra gente uma figura que mostra um campo vetorial e duas curvas sobre ele. Precisamos descobrir se as integrais de linha sobre essas curvas são positivas, negativas ou zero.
Pra isso, vamos analisar a direção da curva e a direção dos vetores de :
- Se a curva estiver sendo percorrida toda no mesmo sentido do campo, o trabalho (e, portanto, a integral de linha sobre ela) é positiva!
- Se estiver sendo percorrida no sentido contrário, é negativa!
- Se em alguns pontos estiver no mesmo sentido e em outros no sentido contrário, pode ser que eles se cancelem (e aí seria zero), ou se os que apontam em um sentido superarem (em quantidade ou em tamanho) o do outro sentido, eles “ganham”.
Uma observação: os vetores que são perpendiculares à curva não contribuem para a integral. Se todos os vetores forem perpendiculares, a integral vale zero!
Então vamos olhar pra imagem, analisando essas direções, pra definir o sinal da integral.
Passo 2
Começando com a curva :
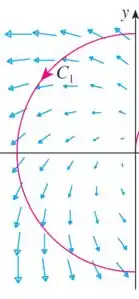
Percebe que tanto o campo quanto a curva estão no sentido anti-horário!
Como os sentidos coincidem, temos que:
Passo 3
Agora pra curva :
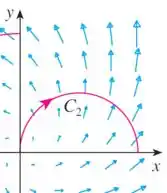
Nesse caso, temos uma mudança ao longo da curva... vou destacar dois vetores pra gente analisar:
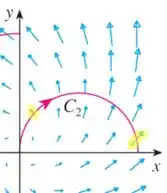
Percebe que esse primeiro vetor (mais à esquerda) está na mesma direção da curva, já que os dois estão apontando pra cima.
Já o segundo vetor (mais à direita) está na direção contrária, ele aponta pra cima e a curva pra baixo.
Bom, isso quer dizer que a integral vai ser zero??
Nesse caso, não!
Analisando os tamanhos: os vetores mais à esquerda, que estão no mesmo sentido de são bem menores que os à direita, que estão no sentido contrário. Então os vetores contrários a superam os que estão na mesma direção e:
Resposta
Integrais de linha positivas para e negativas para .