Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.2 - Ex. 18
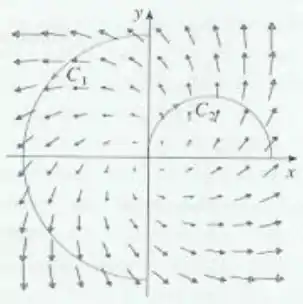
A figura mostra um campo vetorial e duas curvas, e . As integrais de linha de sobre e são positivas, negativas ou nulas? Explique.
Passo 1
Pessoal, se a gente olhar bem, parece que os vetores que começam em seguem mais ou menos o mesmo sentido que o caminho , então temos positivo. Mas,
Ou seja, a integral de linha de sobre deve ser positiva!
Passo 2
Mas pelo contrário, quando a gente olha pra , parece que os vetores que começam em seguem mais ou menos o sentido contrário que o caminho , então temos negativo. Mas,
Ou seja, a integral de linha de sobre deve ser negativa, certo?
Resposta
: positiva
: negativa
Exercícios de Livros Relacionados
Mostre que a integral de linha é independente e calcule a integral. ∫ C ( 2 y 2 - 12 x ³ y ³ )d x + ( 4 x y - 9 x 4 y 2 ) d y ³ ³ C é qualquer caminho de ( 1,1 ) a ( 3,2 )
Determine o trabalho realizado pelo campo de força F → ao mover um objeto de P a Q . F → x , y = 2 y 3 / 2 i → + 3 x y j → ;P 1,1 ,Q ( 2,4 )
Determine o trabalho realizado pelo campo de força F → ao mover um objeto de P a Q . F → x , y = e - y i → - x e - y j → ;P 1,1 ,Q ( 2,0 )
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 1 + x 2 i → + 2 y a r c t g xj → ,C : r → t = t 2 ,2 t , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = x y 2 i → + x 2 y j → ,C : r → t = t + s e n 1 2 π t ,t + cos 1 2 π t , 0 ≤