Seja F o campo vetorial mostrado na figura.(a) Se C 1 é o segmento de reta vertical de - 3 ,- 3 a - 3 ,3 , determine se ∫ C 1 F .d r é positiva, negativa ou zero.(b) Se C 2 é o círculo de raio 3 e centro na origem percorrido no sentido anti-horário, determine se ∫ C 2 F.d r é positiva, negativa ou zero.

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.2 - Ex. 17

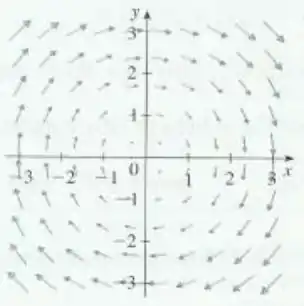
Seja o campo vetorial mostrado na figura.

(a) Se é o segmento de reta vertical de a , determine se é positiva, negativa ou zero.

(b) Se é o círculo de raio e centro na origem percorrido no sentido anti-horário, determine se é positiva, negativa ou zero.

Passo 1

(a) Pessoal, se a gente olhar ao longo da reta , os vetores de têm componentes verticais positivas. Como o caminho do segmento é justamente de baixo para cima, teremos positivo. Mas,

Ou seja, a integral deve ser positiva!

Passo 2

(b) Agora, vamos olhar ao longo da circunferência de raio . Parece que todos os vetores apontam no sentido horário, né mesmo? Como é o círculo percorrido no sentido anti-horário, então será negativo. Analogamente ao item anterior, temos

Ou seja, a integral deve ser negativa, beleza?

Resposta

(a) Positiva.

(b) Negativa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o valor da integral de linha, onde C é a curva dada.

Calcule o valor da integral de linha, onde C é a curva dada. ∫ x + 2 y d x + x 2 d y Em que C é segmento de linha de ( 0,0 ) até ( 2,1 ) e de ( 2,1 ) até ( 3,0 ) .

Calcule o valor da integral de linha, onde C é a curva dada. ∫ x 2 d x + y 2 d y , C consiste no arco de círculo x 2 + y 2 = 4 de ( 2,0 ) até ( 0,2 ) seguido pelo segmento de linha de ( 0,2 ) até ( 4,

Calcule a integral de linha, onde C é a curva dada. ∫ C s e nxd x + cos ⁡ yd y C consiste na metade superior da circunferência x 2 + y 2 = 1 de ( 1 ,0 ) a ( - 1 ,0 ) e o segmento de reta de ( - 1 ,0 )