Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 46
Trace a curva e calcule seu comprimento.
46.
Passo 1
Fala aí! tudo certinho?
Queremos esboçar a curva que tem as equações paramétricas dadas.
E também queremos calcular o comprimento da curva.
Tem ideia de como fazemos isso?
Para resolver esse problema podemos montar uma tabela com os resultados de a partir da variação de . Ou seja, variamos dentro do intervalo e vemos como e se comporta.
Já para determinar o comprimento da curva, usamos a fórmula:
Onde e são os extremos do intervalo de .
Sacou? Bora começar!
Passo 2
Bom, para começar, vamos criar uma tabelinha de valores que relacionam , e , aí poderemos plotar esses pontos no gráfico.
Assim, quando , por exemplo, teremos e . Fazemos o mesmo para os outros valores de e montamos a seguinte tabela:
Show! Agora só precisamos colocar esses pontos em um gráfico e traçar uma linha unindo eles.
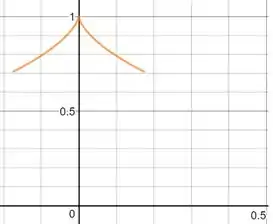
Tranquilo até aqui?
Passo 3
Agora nós queremos calcular o comprimento dessa curva.
Sabemos que o comprimento de uma curva pode ser calculado pela integral:
Então mãos à obra! Vamos calcular
Calculando :
Substituindo em sabendo que e .
Simplificando a função de integração.
Lembra que ? Substituindo dentro da raiz...
Agora temos que lembrar também de outra relação trigonométrica muito importante:
Ou seja...
Tranquilo até aqui?
Passo 4
Como está em módulo, temos que separar a integral em para e para .
Essa mudança de sinal em acontece em , logo:
Calculando as integrais:
Podemos reescrever o resultado como:
É isso! Deu um trabalhinho mas valeu a pena, não é? Responde Aí!