Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 43
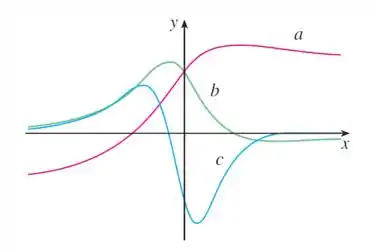
A figura mostra o gráfico de e . Uma é a função posição de um carro, outra é a velocidade do carro e a outra é sua aceleração. Identifique cada curva e explique suas escolhas.
Passo 1
Opa, essa questão é bem legal, temos um quebra cabeças! O enunciado nos da:
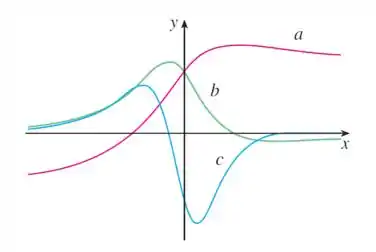
A figura mostra o gráfico de e e diz que uma curva representa a posição de um carro, outra sua velocidade e uma terceira sua aceleração.Mas qual é qual?!
Antes de qualquer coisa temos que lembrar que a velocidade é a variação da posição pela variação de tempo, se o tempo for beeem pequenininho tendendo a zero, então podemos dizer que a onde é a função da posição em relação ao tempo!
Agora, para a aceleração fazemos o mesmo raciocínio, sabendo que a aceleração média é a variação de velocidade em relação ao tempo, portanto . Resumindo temos que :
Sabendo disso podemos analisar as curvas!
Passo 2
Vamos trazer ela pra pertinho da gente:
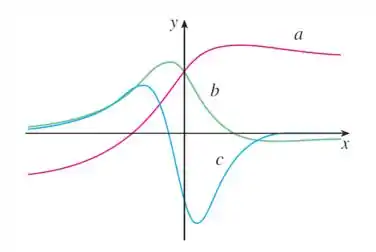
Nesse gráfico o vai significar diferentes coisas, mas o sempre vai ser o tempo! A primeira coisa que podemos observar é que cresce em função de, chega a um máximo e depois começa a descer beeem levemente, ficando quase horizontal.
A gente pode deduzir que considerando que primeiramente o carro esta andando e depois ele começa a andar cada vez mais devagar e em seguida começa a dar ré e continua beeem devagarinho, porque a posição varia muito pouco conforme o tempo passa.
Podemos esperar então uma curva de velocidade crescente inicialmente, chega a um ponto máximo e depois começa a diminuir gradativamente chegando em valores negativos (quando o carro da ré), a velocidade deve voltar a crescer porque o carro continua dando ré, só que é de se esperar que esse finalzinho seja quase horizontal, porque quase não esta variando! A curva que se encaixa com essa descrição é a !
Por eliminação temos , mas vamos conferir se faz sentido! Poderiamos esperar uma aceleração crescente e depois uma queda já que a velocidade começa a diminuir até ficar negativa, depois o carro continua dando ré bem devagarinho, então pelo comportamento das curvas de velocidade que é horizontal no final, esperamos que nesse ponto a aceleração seja zero!
Bate direitinho! Temos então que: