Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 16
15-16 A função descreve a posição de uma partícula movendo-se ao longo de um eixo coordenado, onde está em metros e está em segundos.
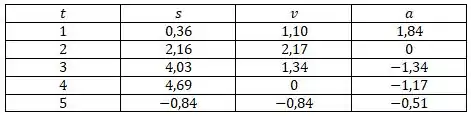
a)Faça uma tabela mostrando a posição, a velocidade e a aceleração com duas casas decimais nos instantes = 1, 2, 3, 4 e 5.
b)Em cada um dos tempos de (a), verifique se a partícula está parada; se não estiver, determine o sentido do movimento.
c) Em cada um dos tempos de (a), verifique se a partícula está aumentando ou diminuindo a velocidade, ou nenhum dos dois.
Passo 1
a)Galerinhaaa, para nós fazermos esse item, temos que lembrar como calculamos a velocidade e a aceleração, né ?
Pronto, agora sim podemos começar !
-Para :
-Para :
-Para :
-Para :
-Para :
Passo 2
b)Galera, aqui nós só temos que lembrar que se a partícula está parada a velocidade dela é zero, e se ela está movendo para direita, mas quando , ela move-se para esquerda.
Assim, a partícula está parada no instante 4, move-se para a direita nos instantes 1,2,3 e está se movendo para a esquerda no instante 5.
Passo 3
c) Aqui, nós só temos que lembrar que se a velocidade e a aceleração tem o mesmo sinal, a partícula está aumentando sua velocidade, caso contrário, sua velocidade está diminuindo. Ok?
Dessa forma, a velocidade aumenta somente nos instantes 1, 5 e, diminui nos instantes 3.
Resposta
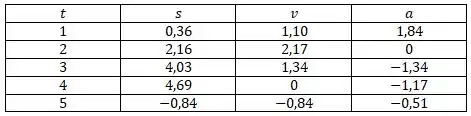
a)
b) A está parada no instante 4, move-se para a direita nos instantes 1,2,3 e está se movendo para a esquerda no instante 5.
c) A velocidade aumenta somente nos instantes 1, 5 e, diminui nos instantes 3.