Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 11

Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região.

y = x 2 , x = y 2 ,   y = 0 ;     e m   t o r n o   d o   e i x o   y = 1

Passo 1

Opa, bora resolver esse problema! O enunciado nos dá as seguintes curvas

y = x 2 , x = y 2 ,   y = 0

E pede pra a gente calcular o volume do sólido obtido pela rotação em torno do eixo y da região delimitada pelas curvas acima! Depois disso temos que esboçar a região!

Antes de qualquer coisa a gente precisa conseguir visualizar o problema. Então vamos esboçar o gráfico das curvas dadas! Temos duas parábols:

y = x 2 → c o n c a v i d a d e   p r a   c i m a ,   p a s s a   p e l a   o r i g e m

x = y 2 → c a v i d a d e   p r a   d i r e i t a ,   p a s s a   p e l a   o r i g e m

E uma reta:

y = 0

Lembrando que seja S um sólido que está entre x = a e x = b . Se a área da secção transversal de S no plano P x , passando por x e perpendicular ap eixo x , é A x , onde A é uma função contínua, então o volume S é dado por:

V = ∫ a b A x d x

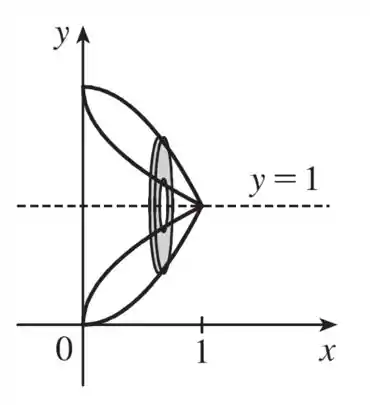
Após encontrar o volume, iremos esboçar graficamente o sólido e a região.

Passo 2

Dadas a equações mencionadas no enunciado temos a seguinte região que será girada em torno do eixo y = 1 é a seguinte:

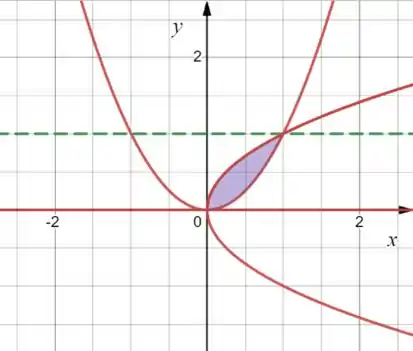
Ali de verde a gente tem y = 1 que é o eixo por onde vamos rotacionar a nossa figura! Podemos ver na figura que a nossa integral terá limites 0 e 1 .

Passo 3

Pra calcular a área fazemos:

A = π r 2

Nesse caso vamos ter dois raios diferentes, já que temos uma área delimitada por duas curvas. Aqui a gente tem que ter um cuidado a mais pois o eixo de rotação não é igual a zero. Pra facilitar a gente olha o gráfico acima e olha a diferença entre cada curva e o eixo y = 1 , assim ficamos com:

r 1 = 1 - x

r 2 = 1 - x 2

Para calcular a área temos:

A ( x ) = π 1 - x 2 - π 1 - x 2 2

O volume é dado pela integral da área:

V = ∫ 0 1 A x d x ∴

V = ∫ 0 1 π 1 - x 2 2 - π 1 - x 2 d x ∴

V = π ∫ 0 1 1 + x 4 - 2 x - 1 + x - 2 x d x ∴

V = π ∫ 0 1 x 4 - 3 x + 2 x d x ∴

Calculando a integral:

π x 5 5 - 3 x 2 2 + 2 x 3 2 3 2 0 1 = π x 5 5 - 3 x 2 2 + 3 4 x 3 2 0 1

π x 5 5 - 3 x 2 2 + 3 4 x 3 2 0 1 = π 1 5 5 - 3 1 2 2 + 3 4 1 3 2 - 0 5 5 - 3 0 2 2 + 3 4 0 3 2

= π 1 5 - 3 2 + 3 4

V = 11 π 30

Passo 4

Esboçando o sólido e disco típico resultantes ao rotacionar a figura em torno do eixo y = 1 , temos:

Resposta

V = 11 π 30

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 π / 2 cos ² ⁡ x . d x ²
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 + sec ⁡ x ,y = 3 ;
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos x = 2 y ,x = 0 ,y = 9 ;e
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. y = x 3 ; y = x ; x ≥ 0 ; Em torno do eixo x .