Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.1 - Ex. 39
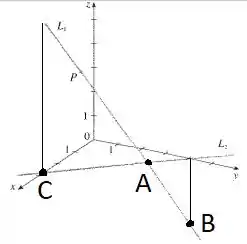
A figura mostra uma reta no espaço e uma segunda reta , que é a projeção de no plano (Isto é, os pontos de estão diretamente embaixo ou em cima dos pontos de ).
- Determine as coordenadas do ponto P da reta .
- Localize no diagrama os pontos e onde a reta intercepta os planos , e .
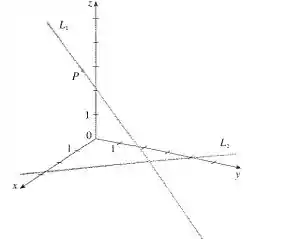
Passo 1
Para fazermos a letra a), precisamos fazer aproximações no gráfico. Projetando o ponto nos eixos , e , vamos obter as coordenadas do ponto. Fazendo isto, temos o seguinte ponto
Passo 2
Já para a letra b), vamos utilizar o desenho como auxilio e traçar retas perpendiculares ao eixo para descobrirmos algumas das interseções com o plano. Seja os pontos , e as interseções da reta com os planos , e respectivamente, temos:
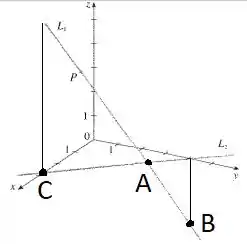
Resposta
Exercícios de Livros Relacionados
Mostre que o triângulo com vértices em P - 2,4 , 0 , Q 1,2 , - 1 e R - 1,1 , 2 é um triângulo equilátero.
Encontre o comprimento do triângulo com vértices A 1 , 2 , - 3 , B 3 , 4 , - 2 e C 3 , - 2 , 1 . O triângulo A B C é retângulo? É isósceles?
Determine se os pontos estão alinhados. A 5,1 , 3 , B 7,9 , - 1 , C 1 , - 15,11 K 0,3 , - 4 , L 1,2 , - 2 , M 3,0 , 1
Determine a equação da esfera com centro em 1 , - 4,3 e raio 5 . Qual é a interseção dessa esfera com o plano x z ?