Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 62
A figura mostra a superfície criada quando o cilindro intercepta o cilindro . Encontre a área desta superfície.
Passo 1
Note que os cilindros e se interceptam ao longo dos planos e . Então podemos tentar encontrar, por meio de uma integral, a área da superfície do cilindro acima do plano , limitada pelos planos no primeiro quadrante, e isso representaria da área total que queremos encontrar.
Passo 2
Para calcular a área de acordo com o descrito no passo anterior, podemos usar a seguinte fórmula:
onde e é a região triangular mostrada na seguinte figura:
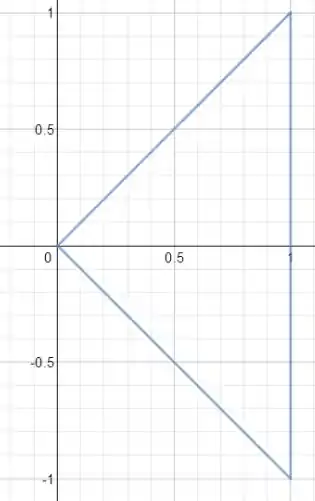
Então,
Passo 3
Show! Agora é só resolver a integral:
Resposta
Exercícios de Livros Relacionados
5 . Calcule a área da parte da superfície esférica x 2+y 2+z 2=1 que seencontra dentro do cone z ≥ x 2 + y ² ²
6 . Calcule a área da superfície z = sqrt(x^2 + y ²) , (x - 2)^2 + 4 y^2 = 1 ²
12 . Calcule a área da parte da superfície z=x y que se encontra dentro docilindro x 2+y 2≤4 e fora do cilindro x 2+y 2≤1
2 . Seja A=0 ,y ,z ∈R 3z 2+y-2 2=1 } ; ache a área da superfíciegerada pela rotação em torno do eixo Oz do conjunto A.
7 . Calcule a área da superfície esférica x 2+y 2+z 2=2 que seencontra dentro do paraboloide z=x 2+y 2