Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 2

2 . Seja A   =   0 ,   y ,   z ∈   R 3   z 2   +   y   -   2 2   =   1 } ; ache a área da superfíciegerada pela rotação em torno do eixo Oz do conjunto A.

Passo 1

Estamos Trabalhando com um toroide aqui. Podemos apenas usar a formula padrão do toroide para calcular essa area que nos diz que

A = 2 π   r   2 π ρ

Que é a ideia básica de rotação de um ponto

Pra apenas um ponto se rotacionarmos temos que essa circunferência terá um comprimento de

C = 2 π r

Como temos um tiroide

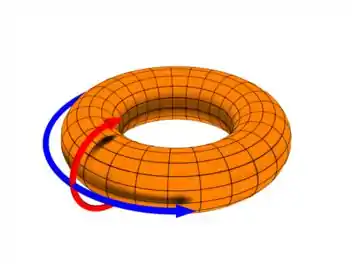
Temos então ao invés de um único ponto um conjunto de pontos que comporão essa nova circunferência. Então será feito o comprimento do arco do tiroide vezes o nosso conjunto de pontos

A = 2 π   r   2 π ρ

Então como saber o raio do toroide ? Esta tudo na equação

z 2   +   y   -   2 2   =   1

Logo

ρ = 2

r = 1

Visto que y   -   2 2   nos diz que o circulo primário esta afastado em 2 unidades

E z 2   +   y   -   2 2   =   1 nos diz que esse circulo primário tem raio 1

Assim nossa area fica

A = 8 π 2

Passo 2

Outra maneira de calcular é usando a parametrização

x = ( ρ + r cos ⁡ v ) sen ⁡ u

y = ( ρ + r cos ⁡ v ) cos ⁡ u

z = r sin ⁡ v

Sendo no nosso caso

ρ = 2

r = 1

E calcular

∫ ∫ S d S =     ∫ ∫ R ∂ A ∂ u × ∂ A ∂ v   d u d v    

Assim esse produto vetorial fica

∂ A ∂ θ × ∂ A ∂ ϕ =   x → y → z → ( 2 + cos ⁡ v ) cos ⁡ u 2 + cos ⁡ v ( - s e n   u ) 0 - s e n   v cos ⁡ u - s e n v cos ⁡ u cos ⁡ v

= ( 2 + cos ⁡ v ) cos ⁡ u - s e n   u ,   - 2 + cos ⁡ v cos ⁡ u   cos ⁡ v ,   2 + cos ⁡ v ( - s e n   v )      

Assim nossa integração fica

∫ ∫ R ∂ A ∂ u × ∂ A ∂ v   d u d v   → ∫ 0 2 π ∫ 0 2 π 2 + cos ⁡ v ) cos ⁡ u - sen u ⁡ ) ²   +     (   - 2 + cos ⁡ v cos ⁡ u   cos ⁡ v ) ²     +   (   2 + cos ⁡ v ( - s e n   v ) 2   d u d v

=   ∫ 0 2 π ∫ 0 2 π 2 + cos ⁡ v   d u d v

As funções cosseno ou seno integradas no intervalo [ 0,2 π ] retornam 0 . Logo Podemos integrar logo em v e assim anular a função cosseno

∫ 0 2 π ∫ 0 2 π 2 + cos ⁡ v   d u d v → ∫ 0 2 π 4 π   d u = 8 π 2

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

A = 8 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8 . Calcule a área da parte do cone z 2=x 2+y 2 que se encontra dentro docilindro x 2+y 2≤2 x , fora do cilindro x 2+y 2≤1 e acima do plano x y .
Calcule a área da parte do paraboloide elíptico z = x 2 + 2 y 2 que se encontra dentro do cilindro 4 x 2 + 16 y 2 ≤ 1 .
Seja K o conjunto do plano x y limitado pelas curvas (em coordenadas polares) ρ = t gθ , 0θπ 2 ,eθ = π 4 . Calcule a área da superfície z = x y , x , y ∈ K .
Seja K o conjunto do plano x y limitado pelas curvas (em coordenadas polares) ρ 2 = cos ⁡ 2 θ , - π 4 ≤ θ ≤ π 4 ,eθ = π 4 . Calcule a área da superfície z = x y , x , y ∈ K .
Calcule ∬ K f x , y , z d S sendo: f x , y , z = x ;σ u , v = u ,v ,u 2 + v ,0 ≤ u ≤ 1eu 2 ≤ v ≤ 1 .