Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 3.Exercícios Propostos - Ex. 10

Sejam O A →   =   ( 1,1 , 3 ) , O B →   =   ( 3,2 , 2 ) e O C →   =   ( 1,0 , - 4 ) .

  1. Ache as coordenadas de todos os vetores determinados pelos pontos O, A, B e C.
  2. Demonstre que os 4 pontos (não necessariamente na ordem dada) são vértices de um trapézio retângulo. Faça um desenho razoável colocando os pontos.
  3. Determine o coseno do maior ângulo do trapézio.

Passo 1

  1. E aí, gente? Vamos resolver mais uma questão? Vamos! O item a) pede para achar as coordenadas de todos os vetores determinados pelos pontos O, A, B e C. Como o enunciado já nos deu O A → , O B → e O C → , só precisamos calcular A B → , A C → e B C → . Não sabemos ainda qual figura geométrica os pontos A, B, C e D representam, mas podemos escrever os vetores que precisamos em termos dos que já conhecemos. Olha só:

    2. A B → = A O → + O B → = - O A → + O B → = -   ( 1,1 , 3 ) +   ( 3,2 , 2 ) = ( 2,1 , - 1 )

    A C → = A O → + O C → = - O A → + O C → = -   ( 1,1 , 3 ) + ( 1,0 , - 4 ) = ( 0 , - 1 , - 7 )

    B C → = B O → + O C → = - O B → + O C → = -     ( 3,2 , 2 ) + ( 1,0 , - 4 ) = ( - 2 , - 2 , - 6 )

    Passo 2

  2. Para desenhar os pontos, vamos dizer que o ponto O está na origem de um sistema cartesiano e desenhar os vetores O A → , O B → e O C → . Assim, teremos os pontos A, B e C e podemos verificar que figura os pontos representam. O desenho fica mais ou menos assim:

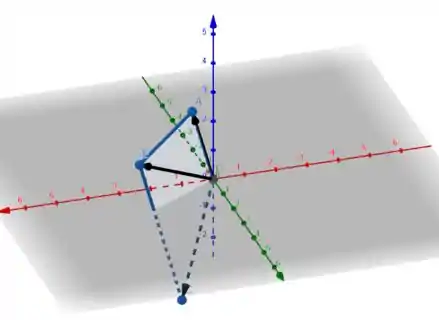
    3. Aqui temos uma visão frontal do paralelogramo, onde a linha representa o plano xy:

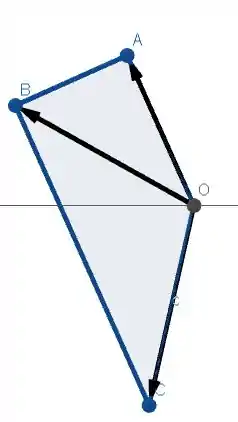
    Passo 3

  3. observando as figuras acima, vemos que o ângulo no vértice O é o maior de todos. Então,

c o s   O   =   O A →   ⋅ O C → | O A → | | O C → | =   ( 1,1 , 3 ) ⋅ ( 1,0 , - 4 ) 1 + 1 + 9 1 + 16 = 1 - 12 11 17 = - 11 11 17 = - 11 17

Resposta

  1. A B → = ( 2,1 , - 1 ) , A C → = ( 0 , - 1 , - 7 ) , B C → = ( - 2 , - 2 , - 6 )
  2. c o s   O   =   - 11 17

Exercícios de Livros Relacionados

Obtenha u → ortogonal a ( 1 ,1 ,0 ) tal que u → = 2 e a medida angular em graus entre u → e ( 1 ,- 1 ,0 ) seja 45 ° .
a) Obtenha os vetores de norma 3 3 que são ortogonais a u → = ( 2 ,3 ,- 1 ) e a v → = ( 2 ,- 4 ,6 ) .b) Qual dos vetores obtidos no item (a) forma ângulo agudo com ( 1 ,0 ,0 ) ?
Descreva o conjunto de todos os vetores w → ortogonais a v → = ( 2 ,1 ,2 ) tais que u → = ( 1 ,1 ,- 1 ) seja combinação linear de v → , w → .
Dados v → = ( 1 ,1 ,1 ) , w → = 0 ,1 ,- 1 e t → = ( 2 ,1 ,- 1 ) , obtenha u → de norma de 5 , ortogonal a t → , tal que ( u → ,v → ,w → ) seja LD.
Obtenha a tripla de coordenadas do vetor que tem norma 3 , é ortogonal a ( 1 ,1 ,0 ) e a ( - 1 ,0 ,1 ) , e forma ângulo obtuso com ( 0 ,1 ,0 ) .