Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 56
A figura a seguir mostra o gráfico de uma função com domínio [-4, 0] e imagem [-3, 0]. Encontre os domínios e as imagens das funções a seguir e esboce os gráficos correspondentes.
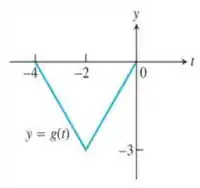
a)
b)
c)
d)
e)
f)
g)
h)
Passo 1
a) Então pessoal, quando a variável está sendo multiplicada por -1, como é o nosso caso, o que acontece é que a função original é refletida em torno do eixo . Caso você não se lembre disso, é só dar uma revisadinha nos livros que eles sempre colocam uma tabelinha lá com essas informações específicas, tudo bem?!
Sendo assim, o gráfico refletido ficaria assim:
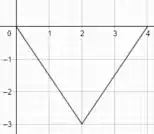
Domínio: [0,4]
Imagem: [-3,0]
Passo 2
b) Aqui temos um caso bem parecido com o da questão a), não é? A diferença é que o -1 não está sendo multiplicado na variável, e sim na função! Nesse caso a reflexão não acontece em torno do eixo e sim em torno do eixo . Dessa forma, o gráfico ficaria assim:
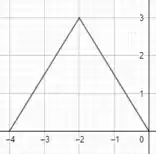
Domínio: [-4,0]
Imagem: [0,3]
Passo 3
c) Gente, como visto no exercício 55, quando há uma soma ou subtração na função, isso significa que a mesma vai ser deslocada para cima ou para baixo. Se for uma soma, o deslocamento vai ser para cima. Se for uma subtração, o deslocamento vai ser para baixo. Tranquilão né?
Como no nosso caso há uma soma de 3 unidades, então a função vai ser deslocada 3 unidades para cima, ficando assim:
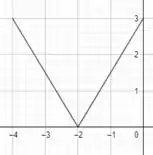
Domínio: [-4,0]
Imagem: [0,3]
Passo 4
d) Nessa questão temos uma junção da questão b) e da questão c). Devido ao sinal negativo na função, isso vai fazer com que ela sofra uma reflexão em torno do eixo . Em seguida, devido à soma de 1 unidade, isso vai fazer com que a função se desloque 1 unidade para cima, ficando assim:
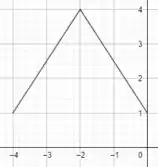
Domínio: [-4,0]
Imagem: [1,4]
Passo 5
e) Essa questão aqui complica um pouquinho as coisas, mas nada impossível, se liga!
De acordo com a questão a), vimos que se há um sinal negativo na variável, isso significa que a função vai ser refletida em torno do eixo . No entanto, ainda temos uma soma dentro da função. Sendo assim, além de ser refletida, a função vai ser deslocada de 2 unidades para a direita, uma vez que agora a função é negativa. Juntando essas informações, teremos um gráfico bem assim:
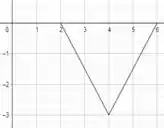
Domínio: [2,6]
Imagem: [-3,0]
Passo 6
f) Nessa questão, pessoal, temos uma subtração de 2 unidades na variável. Quando há uma subtração diretamente na variável, isso significa que a função vai ser deslocada de 2 unidades para a direita. Ah, mas na questão anterior tinha uma soma de 2 unidades e a função também foi para a direita. CUIDADO!
Na questão anterior a função inverteu seus sinais originais, dessa forma o deslocamento também inverte de sentido, sacou?!
Aqui nessa questão não há inversão de sinal, então a regrinha continua válida. Sendo assim, o novo gráfico seria:
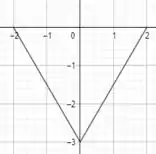
Domínio: [-2,2]
Imagem: [-3,0]
Passo 7
g) Essa questão aqui é idêntica à questão e), gente! A diferença é que não vamos deslocar 2 unidades e sim 1 unidade só. Dessa forma, o gráfico vai ficar assim:
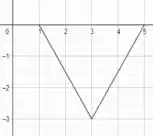
Domínio: [1,5]
Imagem: [-3,0]
Passo 8
h) Por fim, como é de se esperar, temos uma questão um pouco mais chatinha de se resolver, então vamos por partes. Assim como na questão b), sabemos que se há um sinal negativo na função, isso significa que a mesma vai ser refletida em torno do eixo .
Depois de sofrer a reflexão, como há uma subtração de 4 unidades na função, isso significa que a função vai ser deslocada 4 unidades para a direita. Juntando a reflexão e o deslocamento, teremos o seguinte gráfico:
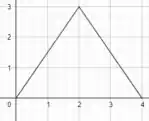
Domínio: [0,4]
Imagem: [0,3]
Resposta
Ei, a resposta está no passo a passo :)