Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.2 - Ex. 8
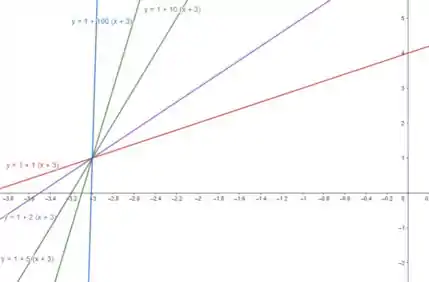
O que todos os membros da família de funções lineares têm em comum? Esboce o gráfico de vários membros da família.
Passo 1
Eaee, belezinha??? Bom... a questão nos dá a seguinte função linear:
E nos pergunta o que todos os membros da família dessa função linear têm em comum.
Para responder isso, temos que saber que uma função linear é dada da seguinte forma:
Em que é o coeficiente angular da reta, ele influencia em quão inclinada nossa reta estará, além de influenciar também se nossa reta será crescente ou decrescente .
Já são pontos pertencentes a reta, esses pontos são utilizados na hora de criarmos a equação da reta, pois são pontos que a gente quer que obrigatoriamente nossa reta contenha.
A partir disso, podemos comparar e responder essa pergunta.
Além disso, a questão pede para esboçarmos o gráfico de para diferentes membros da família.
Para isso, basta atribuirmos valores diferentes de .
E aí?? Bora lá?? 😉
Passo 2
Vamos reorganizar da seguinte forma:
Perceba que, ao comparar com a equação geral da função linear, temos que:
Isso significa que todos os membros dessa família vão passar pelo ponto .
Passo 3
Agora vamos atribuir vários valores de em e analisar o comportamento das funções.
Com uma calculadora gráfica, eu estarei utilizando o GeoGebra, mas fique a vontade para utilizar o que você preferir, então temos:
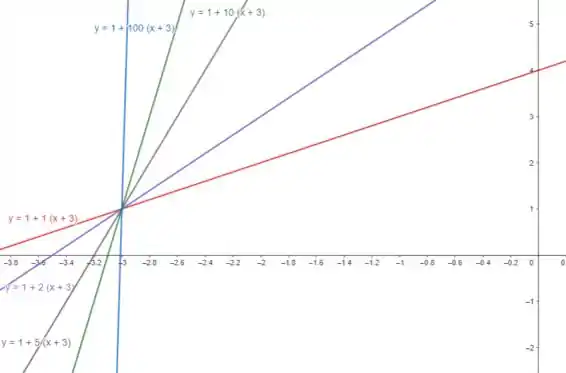
Perceba que todas as retas passam pelo ponto .
Resposta
Todos os membros dessa família vão passar pelo ponto
