Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 20

Um foguete subindo verticalmente é acompanhado por uma estação de radar no solo a 5   k m da rampa de lançamento. Com que rapidez o foguete estará subindo quando sua altura for de 4   k m e sua distância da estação do radar estiver crescendo a uma taxa de 2000   k m / h ?

Passo 1

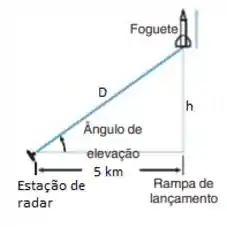
Chamando a distância entre o foguete e a câmera de D , e a altura do foguete num instantengenérico de h , podemos aplicar o teorema de Pitágoras e dizer que:

5 2 + h 2 = D 2

Passo 2

Se a gente derivar essa expressão em relação ao tempo, ficamos com:

d d t ( 5 2 + h 2 ) = d d t ( D 2 )

d 25 d t + d h 2 d t = d D 2 d t  

Como derivada de constante é zero, usando a regra da cadeia:

d h 2 d h d h d t   = d D 2 d D d D d t

2 h d h d t   = 2 D d D d t

Passo 3

O enunciado pergunta a rapidez o foguete estará subindo, ou seja, d h / d t . E nos diz que nesse instante a altura é de 4   k m e sua distância da estação do radar estiver crescendo a uma taxa de 2000   k m / h . Então disso a gente tira que:

h = 4 k m  

d D d t = 2000   k m / h

Além disso, por Pitágoras, conseguimos descobrir o valor de D naquele instante:

5 2 + 4 2 = D 2

D 2 = 41                   ⇒                 D = 41

Passo 4

Substituindo todos esses dados na expressão que a gente encontrou:

2 h d h d t   = 2 D d D d t

2 ( 4 ) d h d t   = 2 ( 41 ) ( 2000 )

d h d t = 500 41   k m / h

Resposta

500 41   k m / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pela ruptura de um navio-tanque, uma mancha de óleo espalha-se em forma de um círculo cuja área cresce a uma taxa constante de 6 k m 2 h . Com que rapidez estará crescendo o raio da mancha quando a ár
Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: x+4 y=3 (a) Dado que d
Em (a) a (d), seja A a área de um círculo de raio r e suponha que r cresça com o tempo t . (a) Faça uma figura do círculo colocando A e r apropriadamente. (b) Escreva uma equação que relacione A e r .
Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: x 2+y 2=2 x+4 y (a) Dad
Tanto x quanto y denotam funções de t que estão relacionadas pela equação dada. Use essa equação e a informação sobre a derivada para encontrar a derivada especificada.Equação: 4 x 2+9 y 2=1 (a) Dado