Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 25
Uma folha de papel retangular É colocada sobre uma superfície plana. Um dos vértices é colocado no lado maior oposto, como mostra a figura, e deixado lá enquanto a folha está aplanada. O problema é tornar o comprimento do vinco o menor possível. Chamamos esse comprimento de . Experimente fazer isso com papel.
Demonstre que
que valor de minimiza
Qual é o valor mínimo de ?
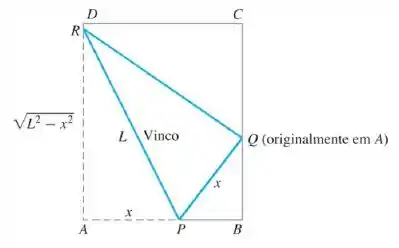
Passo 1
A primeira coisa que temos que ficar atentos é que aquele ponto não fica no topo da folha.
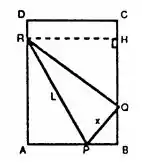
Temos que o triângulo é retângulo em , então:
Além disso, o triângulo é retângulo em , porque é o mesmo ângulo do canto da folha já que ela foi dobrada.
O triângulo também é retângulo, também vamos aplicar Pitágoras ali:
Juntando essas equações, vamos ter:
Se somarmos as , vamos ter:
Ele deu que
Falta acharmos , isso porque temos:
E ele disse na figura que
Passo 2
Pelo triângulo , vamos ter:
Agora, temos que:
Passo 3
Vamos juntar toda essa zona:
Elevando tudo ao quadrado:
Vamos dividir a equação pelo termo sem :
Simplificando em todos os termos:
Se dividirmos todo mundo por , vamos achar o que ele pediu.
Onde vai de até .
Ateção que esse demoninador não pode ser , então
E o não pode ser , se não não teremos dobra.
Passo 4
Letra
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Primeiro fazemos:
Derivando , usando a regra do quociente:
Fazendo isso igual a
Colocando em evidência:
Teremos:
Além disso, temos que ver o valor que a derivada não existe, que é quando o denominador é :
Mas o próprio não vai existir nesse ponto como vimos antes.
Passo 5
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O menor dos valores ,
Passo 6
Letra
O valor mínimo de acontece quando acontece o valor mínimo de